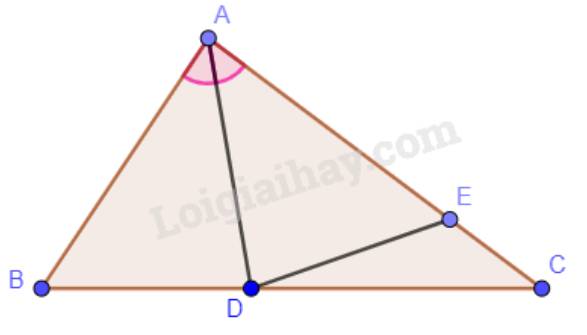
Cho tam giác ABC vuông tại B và \(\widehat{ACB}=30^0\), tia phân giác góc A cắt cạnh BC tại D. Trên cạnh AC lấy E sao cho : AE = AB.
a) Tính số đo các góc\(\widehat{BAC},\widehat{ADC}\)
b) CM : \(\Delta ABD=\Delta AED\)
c) CM : DE là trung trực của đoạn AC

Bài làm
a) Xét ∆ABC vuông tại B có:
^BAC + ^C = 90°
Hay ^BAC + 30° = 90°
=> ^BAC = 60°
Vì AD là phân giác của góc BAC.
=> ^DAC = 60°/2 = 30°
Xét tam giác ADC có:
^DAC + ^ACD + ^ADC = 180°
Hay 30° + 30° + ^ADC = 180°
=> ^ADC = 180° - 30° - 30°
=> ^ADC = 120°
b) Xét tam giác ABD và tam giác AED có:
AB = AE ( gt )
^BAD = ^EAD ( Do AD phân giác )
Cạnh AD chung.
=> ∆ABD = ∆AED ( c.g.c )
c) Vì ∆ABD = ∆AED ( cmt )
=> ^ABD = ^AED = 90°
=> DE vuông góc với AC tại E (1)
Ta có: ^DAC = ^DCA = 30°
=> ∆DAC cân tại D.
=> AD = DC
Xét tam giác DEA và tam giác DEC có:
Góc vuông: ^DEA = ^DEC ( = 90° )
Cạnh huyền AD = DC ( cmt )
Góc nhọn: ^DAC = ^DCA ( cmt )
=> ∆DEA = ∆DEC ( g.c.g )
=> AE = EC
=> E là trung điểm của AC. (2)
Từ (1) và (2) => DE là trung trực của AC ( đpcm )