Cho viên đạn đang bay vs vận vận tốc 10m/s thì nổ thành 2 mảnh. Mảnh 1 chiếm 60% khối lg của quả lựu đạn và tiếp tục bay theo hướng cũ với vận tốc 25m/s. Tốc độ và hướng chuyển động của mảnh thứ 2 là bao nhiêu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



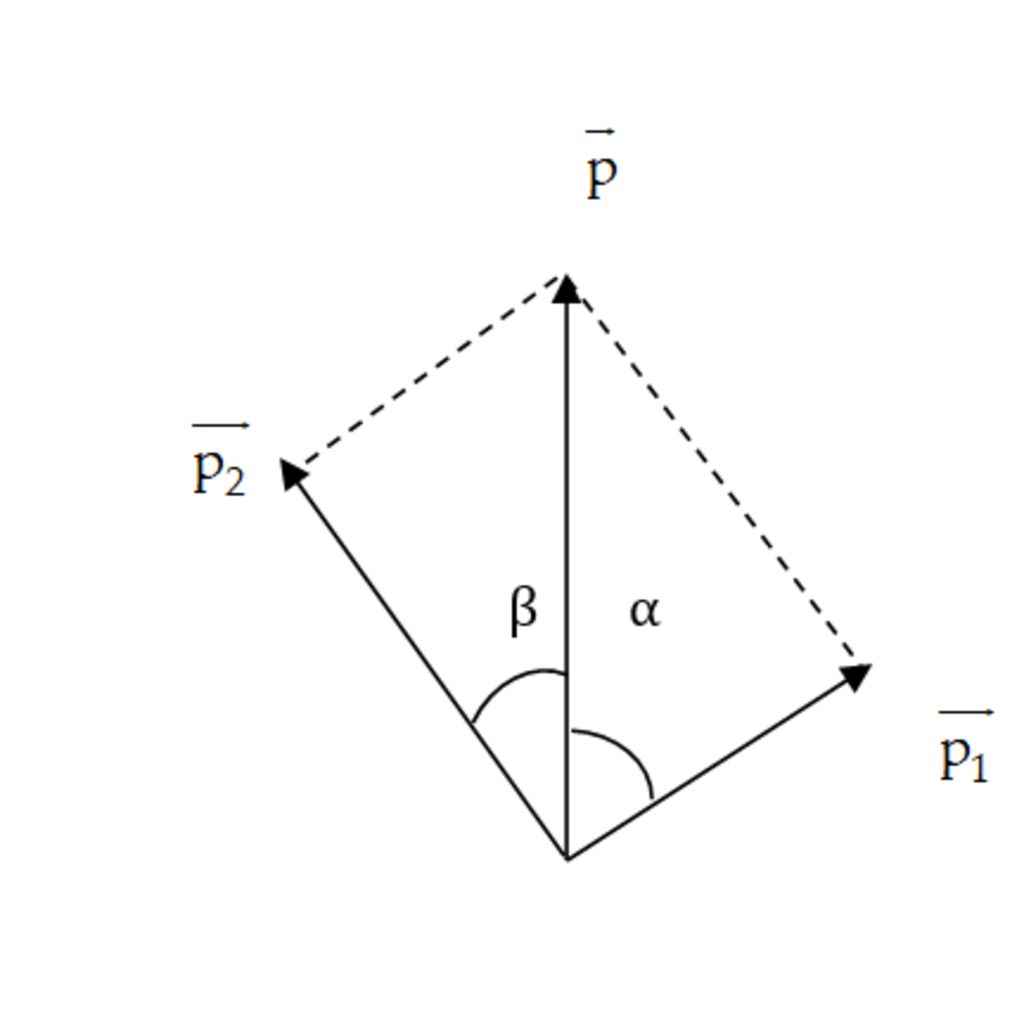
Xét hệ gồm 2 mảnh đạn trong thời gian nổ, đây là hệ kín nên ta áp dụng định luật bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p_h}\)
Trong đó: \(p_h=mv=195\left(kg.m/s\right)\)
\(p_1=m_1v_1=90\sqrt{3}\left(kg.m/s\right)\)
Áp dụng định lý hàm cos: \(p_2=\sqrt{p_1^2+p_h^2-2p_1p_h\cos\left(60^0\right)}\) => v2=p2/m2 =..... tự tính
Gọi \(\beta\) là góc hợp bởi phương ngang và mảnh thứ 2 ta có: \(\cos\beta=\dfrac{p_h^2+p_1^2-p_2^2}{2p_hp_1}=.......\) tự tính nốt :D

Mảnh 1 bay chếch một góc \(60^o\) thì mảnh 2 bay với một góc \(90^o-60^o=30^o\)
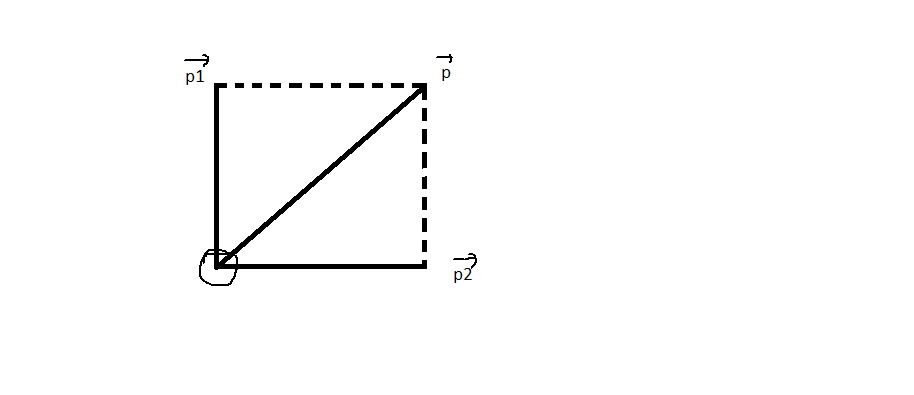
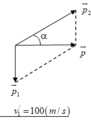
Bảo toàn động lượng:
\(sin60^o=\dfrac{p_1}{p}\Rightarrow p_1=p\cdot sin60^o=mv\cdot sin60^o=\dfrac{m}{2}\cdot v_1\)
\(\Rightarrow v_1=v\sqrt{3}=500\sqrt{3}m\)/s
\(cos30^o=\dfrac{p_2}{p}\Rightarrow p_2=\dfrac{m}{2}\cdot v_2=p\cdot cos30^o=mv\cdot cos30^o\)
\(\Rightarrow v_2=v\sqrt{3}=500\sqrt{3}\)m/s

Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín. Vận tốc mảnh nhỏ trước khi nổ là
v 1 / 2 − v 1 2 = 2 g h ⇒ v 1 = v 1 / 2 − 2 g h ⇒ v 1 = 100 2 − 2.10.125 = 50 3 ( m / s )
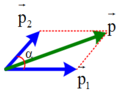
Theo định luật bảo toàn động lượng
p → = p → 1 + p → 2
Với
p = m v = ( 2 + 3 ) .50 = 250 ( k g m / s ) p 1 = m 1 v 1 = 2.50 3 = 100 3 ( k g m / s ) p 2 = m 2 v 2 = 3. v 2 ( k g m / s )
Vì v → 1 ⊥ v → ⇒ p → 1 ⊥ p → theo pitago
⇒ p 2 2 = p 1 2 + P 2 ⇒ p 2 = p 1 2 + p 2 = ( 100 3 ) 2 + 250 2 = 50 37 ( k g m / s )
⇒ v 2 = p 2 3 = 50 37 3 ≈ 101 , 4 ( m / s )
Mà sin α = p 1 p 2 = 100 3 50 37 ⇒ α = 34 , 72 0

Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Vận tốc mảnh nhỏ trước khi nổ là:
v 1 / 2 = v 1 2 = 2 g h ⇒ v 1 = v 1 / 2 − 2 g h
⇒ v 1 = 100 2 − 2.10.125 = 50 3 m / s
+ Theo định luật bảo toàn động lượng: p → = p → 1 + p → 2
Với p = m v = 2 + 3 .50 = 250 k g . m / s
p 1 = m 1 v 1 = 2.50 3 = 100 3 k g . m / s p 2 = m 2 . v 2 = 3. v 2 k g . m / s
+ Vì v → 1 ⊥ v → 2 ⇒ p → 1 ⊥ p → Theo pitago
p 2 2 = p 1 2 + p 2 ⇒ p 2 = p 1 2 + p 2 = 100 3 2 + 250 2 = 50 37 k g . m / s
⇒ v 2 = p 2 3 = 50 37 3 ≈ 101 , 4 m / s + sin α = p 1 p 2 = 100 3 50 37 ⇒ α = 34 , 72 0
Chọn đáp án B

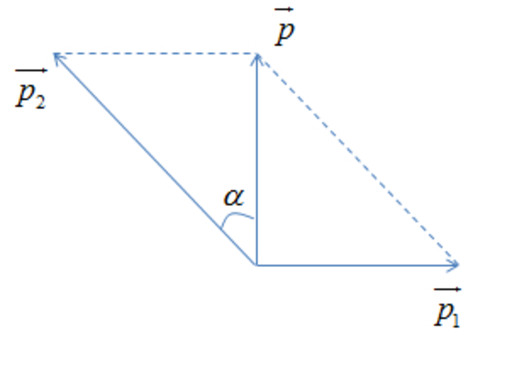
Bảo toàn động lượng ta có:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
\(\Rightarrow p^2=p_1^2+p_2^2+2\cdot p_1\cdot p_2\cdot cos\left(\overrightarrow{p_1;}\overrightarrow{p_2}\right)\) (1)
Có \(p=m\cdot v=2\cdot250=500\)kg.m/s
\(p_1=m_1\cdot v_1=1\cdot250=250kg.\)m/s
\(\left(1\right)\Rightarrow500^2=250^2+p_2^2+2\cdot250\cdot p_2\cdot cos60^o\)
\(\Rightarrow187500=p_2^2+250p_2\)
\(\Rightarrow\left[{}\begin{matrix}p_2\approx325,7\\p_2\approx-575,7\left(loại\right)\end{matrix}\right.\)
Theo hình ta có:
\(p_1\cdot cos\alpha=p_2\cdot sin\beta\)
\(\Rightarrow sin\beta=\dfrac{p_1\cdot cos\alpha}{p_2}=\dfrac{250\cdot cos\left(90-30\right)}{325,7}=0,38\)
\(\Rightarrow\beta\approx22,57^o\)
Mảnh thứ hai bay theo góc \(22,57^o\)

Refer:
\(m=2kg,v=250m/s,v_1=250m/s,α=60^o \)
Động lượng của viên đạn ban đầu:
\(p=m.v=2.250=500kg.m/s\)Động lượng của các mảnh :\(p_1=m_1.v_1=\dfrac{2}{2}.250=250(kg.m/s)\)
\(p_2=m_2.v_2=\dfrac{2}{2}.v_2=v_2(kg.m/s)\)
theo quy tắc hình bình hành ta có:
\(p_2=\sqrt{p_2+p^2_1+2.p.p_1.cosα}\)
\(=\sqrt{500^2+250^2+2.500.250.cos60}\)
\(=661,4(kg.m/s)\)
Vận tốc của mảnh 2:
\(p_2=v_2\Rightarrow v_2=661,4m/s\)Bay theo phương hợp với phương thẳng đứng:\(\dfrac{P}{sin α}=\dfrac{P_1}{sin β} \)
\(\Rightarrow sinβ=\dfrac{sin60.250}{500}=\dfrac{\sqrt{3}}{4} \)
\(\Rightarrow β=25^o39' \)
dạng này mình mới làm xong một bài nhé, bạn có thể lướt xuống tham khảo rồi áp dụng, không nên đăng cùng một loại câu hỏi nhiều lần

