a)Tìm số nguyên biết:
–5 (n + 5)
b)Tính nhanh:
1 – 2 + 3 – 4 + ... + 99 – 100
c)Chứng minh rằng:
5 + 52 + 53 + ...+ 599 + 5100 chia hết cho 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 1 2022
Bài 2:
Ta có: (x-3)(x+4)>0
=>x>3 hoặc x<-4
Bài 3:
a: \(5S=5-5^2+...+5^{99}-5^{100}\)
\(\Leftrightarrow6S=1-5^{100}\)
hay \(S=\dfrac{1-5^{100}}{6}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 11 2023
Đề bài thiếu yêu cầu cụ thể em nhé. em cập nhật lại câu hỏi để được sự hỗ trợ tốt nhất cho tài khoản olm vip
NM
4
BD
29 tháng 6 2023
0\(a.S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ 5S=5-5^2+5^3-5^4+.....+5^{99}-5^{100}\\ 5S+S=\left(5-5^2+5^3-5^4+.....+5^{99}-5^{100}\right)+\left(1-5^{ }+5^2-5^3+.....+5^{98}-5^{99}\right)\\ 6S=1-5^{100}\\ S=\dfrac{1-5^{100}}{6}\\ \)
\(b,S6=1-5^{100}\\ 1-S6=5^{100}\)
=> 5100 chia 6 du 1
AH
Akai Haruma
Giáo viên
13 tháng 12 2022
Lời giải:
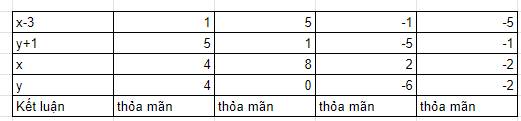
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 12 2023
1/
Gọi d là ước của n+3 và 2n+5 nên
\(n+3⋮d\Rightarrow2n+6⋮d\)
\(2n+5⋮d\)
\(\Rightarrow2n+6-\left(2n+5\right)=1⋮d\Rightarrow d=1\)
=> n+3 và 2n+5 nguyên tố cùng nhau
2/
\(5A=5+5^2+5^3+5^4+...+5^{100}\)
\(4A=5A-A=5^{100}-1\Rightarrow4A+1=5^{100}=\left(5^{50}\right)^2\) LÀ SỐ CHÍNH PHƯƠNG
3/
Tích của 2 số chẵn liên tiếp là
\(2n.\left(2n+2\right)=4n^2+4n=4n\left(n+1\right)\)
Ta có
\(n\left(n+1\right)\) Là tích của 2 số tự nhiên liên tiếp và là số chẵn
\(\Rightarrow n\left(n+1\right)=2k\)
\(\Rightarrow4n\left(n+1\right)=4.2k=8k⋮8\)
NN
9 tháng 11 2017
1)
a)\(B=3+3^3+3^5+3^7+.....+3^{1991}\)
\(\Leftrightarrow B=3\left(1+3^2+3^4+3^6+.....+3^{1990}\right)\)
Vì \(3\left(1+3^2+3^4+3^6+.....+3^{1990}\right)\)chia hết cho 3 nên \(B⋮3\)
\(B=3+3^3+3^5+3^7+.....+3^{1991}\)
\(\Leftrightarrow B=\left(3+3^3+3^5+3^7\right)+.....+\left(3^{1988}+3^{1989}+3^{1990}+3^{1991}\right)\)
\(\Leftrightarrow B=3\left(1+3^2+3^4+3^6\right)+.....+3^{1988}\left(1+3^2+3^4+3^6\right)\)
\(\Leftrightarrow B=3.820+.....+3^{1988}.820\)
\(\Leftrightarrow B=3.20.41+.....+3^{1988}.20.41\)
Vì \(3.20.41+.....+3^{1988}.20.41\) chia hết cho 41 nên \(B⋮41\)
VN
Võ Ngọc Phương
VIP
5 tháng 8 2023
Sửa câu a
a)Ta có:
\(A=3+3^2+3^3+...+3^{99}\)
\(A=\left(3+3^2+3^3\right)+...+\left(3^{97}+3^{98}+3^{99}\right)\)
\(A=\left(3+3^2+3^3\right)+...+3^{96}.\left(3+3^2+3^3\right)\)
\(A=39+...+3^{96}.39\)
\(A=39.\left(1+...+3^{96}\right)\)
Vì 39 \(⋮\) 13 nên 39 . ( 1 + ... + 396 ) \(⋮\) 13
Vậy A \(⋮\) 13
_________
b)Ta có:
\(B=5+5^2+5^3+...+5^{50}\)
\(B=\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{49}+5^{50}\right)\)
\(B=\left(5+5^2\right)+5^2.\left(5+5^2\right)+...+5^{48}.\left(5+5^2\right)\)
\(B=30+5^2.30+...+5^{48}.30\)
\(B=30.\left(1+5^2+...+5^{48}\right)\)
Vì 30 \(⋮\) 6 nên 30. ( 1 + 52 + ... + 548 ) \(⋮\) 6
Vậy B \(⋮\) 6
5 tháng 8 2023
a,A=3+32+33+..+399=(3+32+33)+...+(397+398+399)
=3(1+3+32)+...+397(1+3+32)=3x13+...+397x13=13(3+...+97)⋮13
b,B=5+52+...+550=(5+52)+...+(549+550)=5(1+5)+..+549(1+5)
=5x6+...+549x6=6(5+..+549)⋮6.
23 tháng 6 2015
ta có a=5k+3
Nên a2= (5k+3)2=25k2+30k+9=25k2+30k+5+4=5(5k2+6k+1)+4 chia cho 5 dư 4 (dpcm)
Câu a mk ko hiểu gì nha xl bn nhìu
b)1-2+3-4+...+99-100
=(1-2)+(3-4)+...+(99-100)
=(-1)+(-1)+...+(-1)
=(-1) . 50
=(-50)
c) 5 + 52 + 53 + ...+ 599 + 5100
=(5+52)+(53+54)+....+(599+5100)
=30+52(5+52)+...+598(5+52)
=30.1+52.30+.....+598.30
=30(1+52+...+598) chia hết cho 6