Tập nghiệm của phương trình:
3x + 4x > \(-\frac{11}{3}\)
Ngoài cách giải vẽ đồ thị thì câu này còn cách làm nào khác không ạ ?
Tập nghiệm của phương trình:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 3 2022
a: Thay x=-2 vào pt,ta được:
-8+4a+8-4=0
=>4a-4=0
hay a=1
b: Pt sẽ là \(x^3+x^2-4x-4=0\)
\(\Leftrightarrow x^2\left(x+1\right)-4\left(x+1\right)=0\)
=>(x+1)(x-2)(x+2)=0
hay \(x\in\left\{-1;2;-2\right\}\)
30 tháng 4 2023
Ta có /2x/= 2x nếu 2x≥0 hay x≥0
= -(2x) nếu 2x<0 hay x<0
Phương trình 2x-2=0 với điều kiện x≥0
Ta có 2x-2=0 <=>2x=2 <=>x=2/2 <=>x=1(thỏa mãn điều kiện)
Phương trình -(2x)-2=0 với điều kiện x<0
Ta có -2x-2=0 <=>-2x=2 <=>x=-1(thỏa mãn điều kiện)
Tập nghiệm phương trình S={1;-1}
CM
14 tháng 1 2019
- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x2 – 3x + 6 = x + 3 ⇔ x2 – 4x + 3 = 0.
- Nghiệm của phương trình x2 – 4x + 3 = 0 là: x1 = 1; x2 = 3
x1 có thỏa mãn điều kiện nói trên
x2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1
CM
12 tháng 12 2017
- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x 2 – 3 x + 6 = x + 3 ⇔ x 2 – 4 x + 3 = 0 .
- Nghiệm của phương trình x 2 – 4 x + 3 = 0 l à : x 1 = 1 ; x 2 = 3
x 1 có thỏa mãn điều kiện nói trên
x 2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1
CM
5 tháng 9 2019
x = 2 2 x - y = 3
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
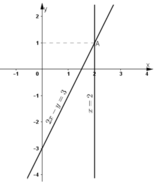
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
8 tháng 2 2022
a) \(3x-11=0\)
\(\Rightarrow3x=11\Rightarrow x=\dfrac{11}{3}\approx3,667\)
b) \(12+7x=0\)
\(\Rightarrow7x=-12\Rightarrow x=-\dfrac{12}{7}\approx-1,714\)
c) \(10-4x=2x-3\)
\(\Rightarrow2x+4x=10+3\Rightarrow6x=13\Rightarrow x=\dfrac{13}{6}\approx2,167\)