Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
Do đó: AMDN là hình chữ nhật
mà AD là tia phân giác
nên AMDN là hình vuông
Xét tứ giác AMDN, ta có: ∠ (MAN) = 90 0 (gt)
DM ⊥ AB (gt)
⇒ ∠ (AMD) = 90 0
DN ⊥ AC (gt) ⇒ ∠ (AND) = 90 0
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông
bạn tự vẽ hình nk.
cm: vì m, n lần lượt là chân đg vuông góc kẻ từ d dến ab,ac
=> tứ giác AMDN là hình chữ nhật (có 3 góc vuông) (dh nb hcn)
mặt #: ad là đg phân giác của góc a
=> hcn AMDN là hình vuông vì có có đường chéo là đường phân giác của góc a(dh nb hv)
Xét tứ giác AMDN, ta có: ∠∠(MAN) = 900900 (gt)
DM ⊥ AB (gt)
⇒∠∠(AMD) = 900900
DN ⊥ AC (gt) ⇒∠∠(AND) = 900900
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
Vì M, N là chân đường vuông góc kẻ từ D đến AB, AC =>tứ giác AMDN là hình chữ nhật (có 3 góc vuông).
(gt) =>AMDN là hình chữ nhật.
(gt) =>AMDN là hình vuông(đpcm).
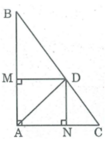
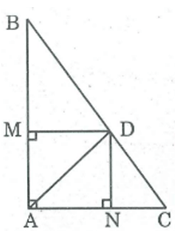
\(\text{GIẢI :}\)
Chứng minh :
Ta có : M là chân đường vuông góc kẻ từ A đến AB \(\Rightarrow\text{ }\widehat{\text{M}}=90^{\text{o}}\).
N là chân đường vuông góc kẻ từ A đến AC \(\Rightarrow\text{ }\widehat{\text{N}}=90^{\text{o}}\)
Xét \(\diamond\text{AMDN}\) có \(\widehat{\text{A}}=\widehat{\text{M}}=\widehat{\text{N}}=90^{\text{o}}\)\(\Rightarrow\text{ }\diamond\text{AMDN}\) là hình chữ nhật.
mà AD là đường phân giác của góc A \(\Rightarrow\text{ }\diamond\text{AMDN}\) là hình vuông.