Cho tam giác ABC ,AB-12cm,AC=18cm,vẽ đường phân giác AD.Điểm I thuộc đoạn thẳng AD sao cho AI=21D.Gọi E là giao điểm của BI và AC.
a.Tính tỉ số \(\frac{AE}{EC}\)
b.Tính độ dài AE,EC?
Các bạn giúp mìn với nha:((((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{DC}=\dfrac{AB}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{BD}{DC}=\dfrac{2}{3}\)
\(\Leftrightarrow\dfrac{BD}{2}=\dfrac{CD}{3}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{2}=\dfrac{CD}{3}=\dfrac{BD+CD}{2+3}=\dfrac{BC}{5}\)
\(\Leftrightarrow\dfrac{BD}{BC}=\dfrac{2}{5}\)
Kẻ DK//BE(K∈EC)
Xét ΔADK có
I∈AD(gt)
E∈AK(gt)
IE//DK(gt)
Do đó: \(\dfrac{AE}{EK}=\dfrac{AI}{ID}\)(Định lí Ta lét)
hay \(\dfrac{AE}{EK}=2\)
Xét ΔBEC có
D∈BC(gt)
K∈EC(gt)
DK//BE(gt)
Do đó: \(\dfrac{EK}{EC}=\dfrac{BD}{BC}\)(Hệ quả của Định lí Ta lét)
hay \(\dfrac{EK}{EC}=\dfrac{2}{5}\)
Ta có: \(\dfrac{AE}{EK}\cdot\dfrac{EK}{EC}=\dfrac{AE}{EC}\)
\(\Leftrightarrow\dfrac{AE}{EC}=2\cdot\dfrac{2}{5}=\dfrac{4}{5}\)
b) Ta có: \(\dfrac{AE}{EC}=\dfrac{4}{5}\)(cmt)
nên \(\dfrac{AE}{4}=\dfrac{EC}{5}\)
mà AE+EC=AC(E nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{4}=\dfrac{EC}{5}=\dfrac{AE+EC}{4+5}=\dfrac{18}{9}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{AE}{4}=2\\\dfrac{EC}{5}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AE=2\cdot4=8\left(cm\right)\\EC=2\cdot5=10\left(cm\right)\end{matrix}\right.\)
Vậy: AE=8cm; EC=10cm

a) Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên BDDC=ABACBDDC=ABAC(Tính chất đường phân giác của tam giác)
⇔BDDC=23⇔BDDC=23
⇔BD2=CD3⇔BD2=CD3
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
BD2=CD3=BD+CD2+3=BC5BD2=CD3=BD+CD2+3=BC5
⇔BDBC=25⇔BDBC=25
Kẻ DK//BE(K∈EC)
Xét ΔADK có
I∈AD(gt)
E∈AK(gt)
IE//DK(gt)
Do đó: AEEK=AIIDAEEK=AIID(Định lí Ta lét)
hay AEEK=2AEEK=2
Xét ΔBEC có
D∈BC(gt)
K∈EC(gt)
DK//BE(gt)
Do đó: EKEC=BDBCEKEC=BDBC(Hệ quả của Định lí Ta lét)
hay EKEC=25EKEC=25
Ta có: AEEK⋅EKEC=AEECAEEK⋅EKEC=AEEC
⇔AEEC=2⋅25=45⇔AEEC=2⋅25=45
b) Ta có: AEEC=45AEEC=45(cmt)
nên AE4=EC5AE4=EC5
mà AE+EC=AC(E nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
AE4=EC5=AE+EC4+5=189=2AE4=EC5=AE+EC4+5=189=2
Do đó:
⎧⎪ ⎪⎨⎪ ⎪⎩AE4=2EC5=2⇔{AE=2⋅4=8(cm)EC=2⋅5=10(cm){AE4=2EC5=2⇔{AE=2⋅4=8(cm)EC=2⋅5=10(cm)
Vậy: AE=8cm; EC=10cm

a) Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên BDDC=ABACBDDC=ABAC(Tính chất đường phân giác của tam giác)
⇔BDDC=23⇔BDDC=23
⇔BD2=CD3⇔BD2=CD3
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
BD2=CD3=BD+CD2+3=BC5BD2=CD3=BD+CD2+3=BC5
⇔BDBC=25⇔BDBC=25
Kẻ DK//BE(K∈EC)
Xét ΔADK có
I∈AD(gt)
E∈AK(gt)
IE//DK(gt)
Do đó: AEEK=AIIDAEEK=AIID(Định lí Ta lét)
hay AEEK=2AEEK=2
Xét ΔBEC có
D∈BC(gt)
K∈EC(gt)
DK//BE(gt)
Do đó: EKEC=BDBCEKEC=BDBC(Hệ quả của Định lí Ta lét)
hay EKEC=25EKEC=25
Ta có: AEEK⋅EKEC=AEECAEEK⋅EKEC=AEEC
⇔AEEC=2⋅25=45⇔AEEC=2⋅25=45
b) Ta có: AEEC=45AEEC=45(cmt)
nên AE4=EC5AE4=EC5
mà AE+EC=AC(E nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
AE4=EC5=AE+EC4+5=189=2AE4=EC5=AE+EC4+5=189=2
Do đó:
⎧⎪ ⎪⎨⎪ ⎪⎩AE4=2EC5=2⇔{AE=2⋅4=8(cm)EC=2⋅5=10(cm){AE4=2EC5=2⇔{AE=2⋅4=8(cm)EC=2⋅5=10(cm)
Vậy: AE=8cm; EC=10cm

Bài 1:

Áp dụng tính chất đường phân giác của tam giác ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{18}=\frac{2}{3}\)
\(\Rightarrow\frac{BD}{2}=\frac{DC}{3}=\frac{BD+DC}{2+3}=\frac{BC}{5}\Rightarrow\frac{BD}{BC}=\frac{2}{5}\)
Kẻ \(DK//BE\left(K\in AC\right)\text{ ta có:}\)
\(\frac{AE}{EK}=\frac{AI}{ID}=2;\frac{EK}{EC}=\frac{BD}{BC}=\frac{2}{5}\)
Do đó:\(\frac{AE}{EK}\cdot\frac{EK}{EC}=\frac{AE}{EC}=\frac{2}{5}.2=\frac{4}{5}\)
b)\(\text{Ta có:}\)
\(\frac{AE}{EC}=\frac{4}{5}\Rightarrow\frac{AE}{4}=\frac{EC}{5}=\frac{AE+EC}{4+5}=\frac{AC}{9}=\frac{18}{9}=2\)
\(\Rightarrow AE=8cm,EC=10cm\)
bn ơi bài 1 ý a) chỉ có thể tính tỉ lệ thôi ko tính đc ra số hẳn đâu

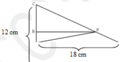
Nối AF ta nhận thấy AE cũng bằng đường cao của tam giác FAB ( vì EF song song với AB).
Theo đầu bài: AF = 1 2 E C hay A E = 1 3 A C = 12 3 = 4 c m
Vậy S F A B = 18 x 4 2 = 36 ( c m 2 )
S A B C = 18 x 12 2 = 108 ( c m 2 ) S F A C = 108 − 36 = 72 ( c m 2 )
Nên suy ra: E F = 72 x 12 2 = 12 ( c m ) vì EF song song với AB nên EF chính là đường cao của tam giác FAC. Vậy EF = 12(cm).
Vì EF song song với AB nên EF chính là đường cao của tam giác FAC
Nối AF ta nhận thấy AE cũng bằng đường cao của tam giác FAB ( vì EF song song với AB).
Theo đầu bài: AF = 1 2 E C hay A E = 1 3 A C = 12 3 = 4 c m
Vậy S F A B = 18 x 4 2 = 36 ( c m 2 )
S A B C = 18 x 12 2 = 108 ( c m 2 ) S F A C = 108 − 36 = 72 ( c m 2 )
Nên suy ra: E F = 72 x 12 2 = 12 ( c m ) vì EF song song với AB nên EF chính là đường cao của tam giác FAC. Vậy EF = 12(cm).
Vì EF song song với AB nên EF chính là đường cao của tam giác FAC