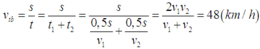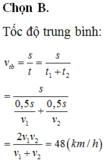Một chiếc xe ô tô di chuyển trên quãng đường từ A tới B với vận tốc trung bình là 50km/h mất 60 phút đồng hồ. Xe di chuyển từ A tới I ( biết I là một điểm bất kì nằm trên đoạn đường AB ) với vận tốc trung bình 60km/h trong khoảng thời gian 20 phút. Hỏi trên đoạn đường IB xe chạy với vận tốc trung bình bằng bao nhiêu ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 8 2021
Vận tốc của nửa quãng đg sau là:
Ta có:\(v_{tb}=\dfrac{s_1+s}{t_1+t}=\dfrac{s}{\dfrac{s}{2v_1}+\dfrac{s}{2v}}=\dfrac{2v_1v}{v_1+v}\Rightarrow v_{tb}.v_1+v_{tb}.v=2v_1v\)
\(\Leftrightarrow v_{tb}.v_1=v\left(2v_1-v_{tb}\right)\Leftrightarrow v=\dfrac{v_{tb}.v_1}{2v_1-v_{tb}}=\dfrac{30.36}{2.36-30}=25,71\left(km/h\right)\)
VT
12 tháng 6 2017
Chọn đáp án A
? Lời giải:
− Thời điểm xe tới A là: t = 6 giờ + 2,5 giờ + 30 phút + 2 giờ =11 giờ
17 tháng 10 2023
Thời gian xe lúc đi: \(t_1=\dfrac{120}{48}=2,5h\)
Thời gian xe nghỉ: \(\Delta t=30min=\dfrac{1}{2}h\)
Thời gian xe lúc về: \(t_2=\dfrac{120}{60}=2h\)
Tổng thời gian đi: \(t=t_1+\Delta t+t_2=2,5+\dfrac{1}{2}+2=5h\)
Xe tới A lúc \(6+5=11(giờ)\)
XO
11 tháng 2 2021
Đổi 20m/s = 72km/h
Ta có Vtb = \(\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{2.v_1}+\frac{S}{2.v_2}}=\frac{S}{\frac{S}{2}\left(\frac{1}{v_1}+\frac{1}{v_2}\right)}=\frac{1}{\frac{1}{2}\left(\frac{v_1+v_2}{v_1.v_2}\right)}=\frac{2.v_1.v_2}{v_1+v_2}=\frac{2.50.72}{50+72}=59,01\)km/h
11 tháng 2 2021
Thời gian đi trên nửa đoạn đường đầu là:
\(t_1=\dfrac{AB}{2v_1}=\dfrac{AB}{2.50}=\dfrac{AB}{100}\left(h\right)\)
Thời gian đu trên nửa đoạn đường sau là:
\(t_2=\dfrac{AB}{2v_2}=\dfrac{AB}{2.20}=\dfrac{AB}{40}\left(h\right)\)
Vận tốc trung bình trên cả quãng đường AB là:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{AB}{\dfrac{AB}{100}+\dfrac{AB}{40}}=\dfrac{AB}{AB\left(\dfrac{1}{100}+\dfrac{1}{40}\right)}=\dfrac{1}{\dfrac{1}{100}+\dfrac{1}{40}}=\dfrac{200}{7}\approx28,57\left(km/h\right)\)