Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Kẻ đường cao AH. Vẽ HE, HF vuông góc với AB, AC
a) Tính độ dài các đoạn thẳng BC, AH, EF
b) Gọi M, N lần lượt là trung điểm của HB và HC. Tứ giác MNFE là hình gì? Tính diện tích tứ giác MNFE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 12 2020
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay \(BC=\sqrt{100}=10cm\)
Xét ΔABC có AH là đường cao ứng với cạnh BC nên
\(S_{ABC}=\dfrac{AH\cdot BC}{2}\)(1)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}\)(2)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay \(AH=\dfrac{48}{10}=4.8cm\)
Vậy: AH=4,8cm
b) Xét tứ giác AEHF có
\(\widehat{EAF}=90^0\)(ΔABC vuông tại A, E∈AB, F∈AC)
\(\widehat{AEH}=90^0\)(HE⊥AB)
\(\widehat{AFH}=90^0\)(HF⊥AC)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
⇒AH=EF(Hai đường chéo của hình chữ nhật AEHF)
mà AH=4,8cm(cmt)
nên EF=4,8cm
Vậy: EF=4,8cm
CM
28 tháng 7 2017
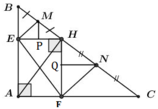
Kẻ MP ⊥ EH (P Є EH), NQ ⊥ HF (Q Є HF) ta có:
MP và NQ lần lượt là đường trung bình của tam giác HBE và HFC
nên MP = 1 2 BE, NQ = 1 2 FC
S Δ M E H = 1 2 M P . E H = 1 2 . 1 2 B E . E H = 1 2 . S Δ H B E
S Δ H N F = 1 2 N Q . H F = 1 2 . 1 2 C F . H F = 1 2 S Δ H C F
S Δ H E F = 1 2 S Δ A E H F
=> SEMNF = 1 2 (SHBE + SHCF + SAEHF)
= SABC = 1 2 .AB. 1 2 AC = 1 4 .6.8 = 12 (cm2)
Đáp án cần chọn là: C