Các bạn giải hộ mình bài hình này với !? Mình đang cần gấp ạ :>
Đề bài : Cho tam giác ABC cân tại A có góc BAC = 80 độ, kẻ đường cao BE và CD cắt nhau tại O
a, Chứng minh : \(\Delta\)EBA = \(\Delta\)DCA và tính góc ABE, góc ABC
b, Chứng minh AO là tia phân giác góc BAC
c, Gọi BM và CN lần lượt là các tia phân giác của góc kề bù với góc BAC và góc ACB, F là giao điểm của BM và CN . Chứng minh 3 điểm A, O, F thẳng hàng
Thankss ạ. Mình sẽ tik cho các bạn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình bạn tự vẽ nhé
a. ví tam giác ABC là tam giác cân và có góc A bằng 90 độ nên tam giác ABC là tam giác vuông cân tại A
=> góc BAC = 90 độ và AB=AC
Xét tứ giác ABIC có góc BAC =90 độ, góc ABI = 90 độ (vì AIvuông góc với AB ), góc ACI =90độ (vì AC vuông góc với CI)
=> tứ giác ABIC là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
mà AB=AC (cmt)
=> Tứ giác ABIC là hình vuông (dấu hiệu nhận biết hình vuông)
=> AI là phân giác góc BAC

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: góc ABH+góc EBC=góc ABC
góc ACK+góc ECB=góc ACB
mà góc ABH=góc ACK;góc ABC=góc ACB
nên góc EBC=góc ECB
=>ΔEBC cân tại E
c: AB=AC
EB=EC
=>AE là trung trực của BC
=>AE vuông góc với BC

a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
b: Sửa đề; HE*HB=HF*HC
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HE*HB=HF*HC
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc AO

Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC

Giải thích các bước giải:
a) ΔABCΔABC có đường cao AN,BMAN,BM
⇒AN⊥BC;BM⊥AC⇒AN⊥BC;BM⊥AC
Xét tứ giác IMCNIMCN có:
ˆIMC=ˆINC=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)IMC^=INC^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
⇒ˆIMC+ˆINC=1800⇒IMC^+INC^=1800
⇒⇒ tứ giác IMCNIMCN nội tiếp
b) Xét ΔBINΔBIN và ΔAIMΔAIM có:
ˆBNI=ˆAMI=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)BNI^=AMI^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
ˆBIN=ˆAIMBIN^=AIM^ (đối đỉnh)
⇒⇒ ΔBIN∽ΔAIMΔBIN∽ΔAIM (g.g)
⇒IBIA=INIM⇒IA.IN=IM.IB⇒IBIA=INIM⇒IA.IN=IM.IB
c) Tứ giác IMCNIMCN nội tiếp
⇒ˆAIH=ˆNCM⇒AIH^=NCM^ hay ˆAIH=ˆACBAIH^=ACB^
Xét (O)(O) có: ˆACB=ˆAHBACB^=AHB^ (2 góc nội tiếp cùng chắn cung ABAB)
⇒ˆAIH=ˆAHB⇒AIH^=AHB^
⇒ˆAIH=ˆAHI⇒ΔAIH⇒AIH^=AHI^⇒ΔAIH cân tại A⇒AI=AH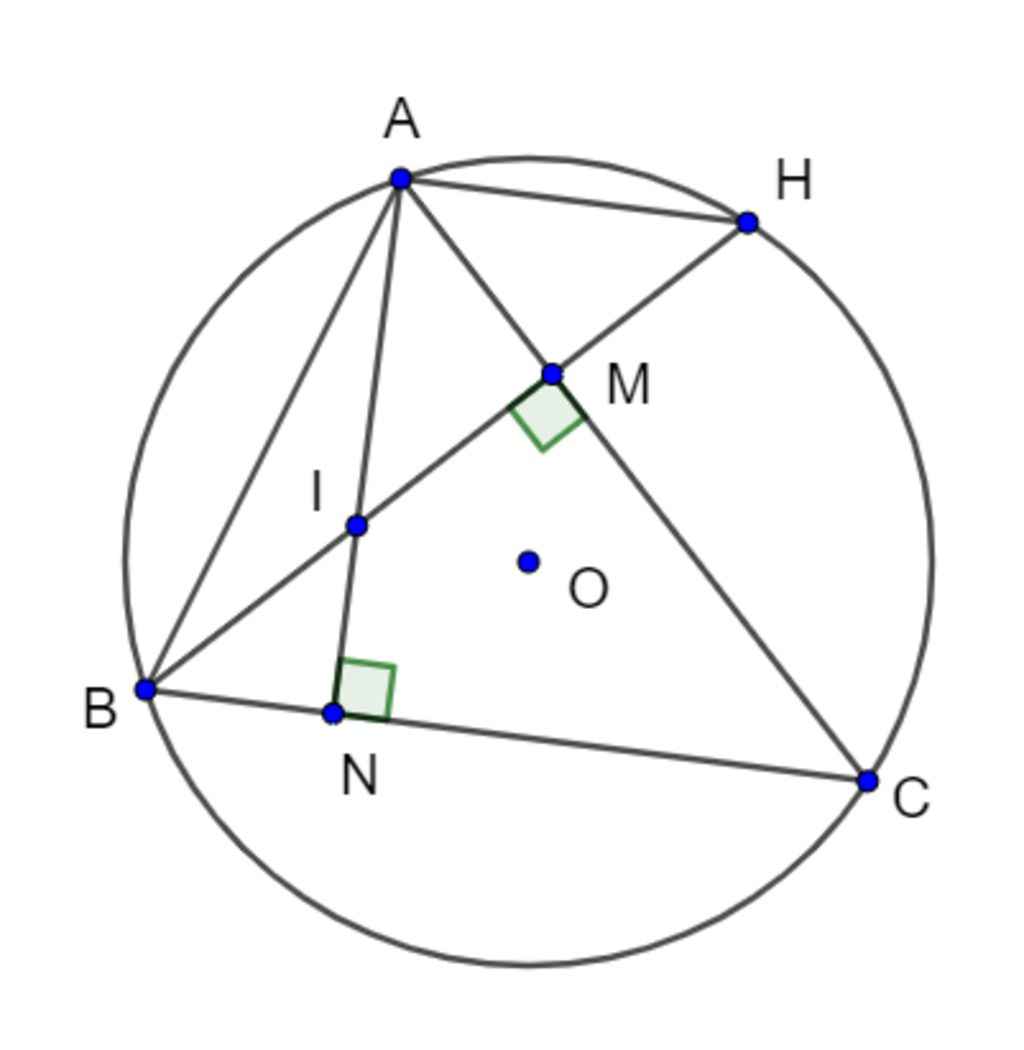

Bài 3 :
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)


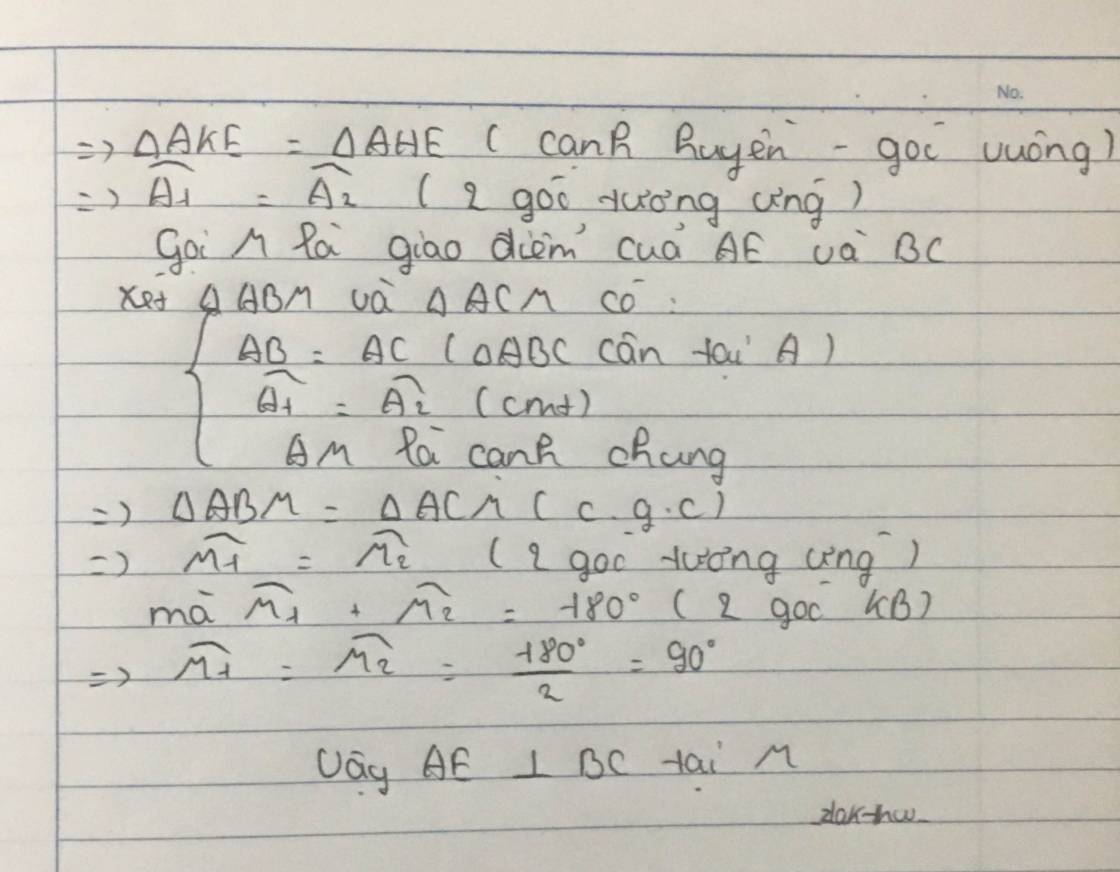
a, Vì △ABC cân tại A => AB = AC và ∠ABC = ∠ACB = (180o - ∠BAC) : 2 = (180o - 80o) : 2 = 100o : 2 = 50o
Xét △ABE vuông tại E có: ∠ABE + ∠BAE = 90o (tổng 2 góc nhọn trong △ vuông)
=> ∠ABE + 80o = 90o => ∠ABE = 10o
Xét △EBA vuông tại E và △DCA vuong tại D
Có: AB = AC (cmt)
∠BAC là góc chung
=> △EBA = △DCA (ch-gn)
b, Vì △EBA = △DCA (cmt) => AE = AD (2 cạnh tương ứng) và ∠ABE = ∠ACD (2 góc tương ứng)
Ta có: AD + BD = AB và AE + EC = AC
Mà AD = AE (cmt) ; AB = AC (cmt)
=> BD = EC
Xét △BDO vuông tại D và △CEO vuông tại E
Có: BD = EC (cmt)
∠DBO = ∠ECO (cmt)
=> △BDO = △CEO (cgv-gnk)
=> BO = OC (2 cạnh tương ứng)
Xét △BAO và △CAO
Có: AB = AC (cmt)
BO = OC (cmt)
AO là cạnh chung
=> △BAO = △CAO (c.c.c)
=> ∠BAO = ∠CAO (2 góc tương ứng)
Mà AO nằm giữa AB, AC
=> AO là tia phân giác ∠BAC
c, Sửa đề: Gọi BM và CN.... góc kề bù với ∠ABC và ∠ACB
Gọi góc kề bù với ∠ABC và ∠ACB lần lượt là: ∠CBx và ∠BCy
Ta có: ∠ABC + ∠CBx = 180o (2 góc kề bù) và ∠ACB + ∠BCy = 180o (2 góc kề bù)
Mà ∠ABC = ∠ACB (cmt)
=> ∠CBx = ∠BCy (1)
Vì BM là phân giác CBx => ∠CBM = ∠MBx = ∠CBx : 2 (2)
Vì CN là phân giác ∠BCy => ∠BCN = ∠NCy = ∠BCy : 2 (3)
Từ (1) ; (2) ; (3) => ∠BCN = ∠CBM
Xét △BCF có: ∠BCF = ∠FBC (cmt) => ∠BCF cân tại F => BF = FC
Xét △ABF và △ACF
Có: AB = AC (cmt)
BF = FC (cmt)
AF là cạnh chung
=> △ABF = △ACF (c.c.c)
=> ∠BAF = ∠CAF (2 góc tương ứng)
=> AF là tia phân giác góc BAC
Mà AO là tia phân giác góc BAC
=> AF ≡ AO
=> 3 điểm A, O, F thẳng hàng
Cảm ơn bạn Nhật Hạ nha \(\omega\)