Số đo ba góc A, B, C của tam giác ABC tỉ lệ với 5, 2, 3. AH là đường cao của tam giác ABC. Khi đó góc BAH bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong tam giác BAH có ∠(BAH) + ∠(AHB) + ∠(ABH) = 180o
⇒∠(BAH) = 180o - 90o - 50o = 40o
Chọn A

Trong tam giác BAH có ∠(BAH) + ∠(AHB) + ∠(ABH) = 180o
⇒∠(BAH) = 180o - 90o - 50o = 40o
Chọn A

\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=60^0\\\widehat{C}=84^0\end{matrix}\right.\)

Trong tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \)
Mà số đo ba góc \(\widehat A,\widehat B,\widehat C\) của tam giác ABC tỉ lệ với 5;6;7 nên \(\dfrac{{\widehat A}}{5} = \dfrac{{\widehat B}}{6} = \dfrac{{\widehat C}}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\dfrac{{\widehat A}}{5} = \dfrac{{\widehat B}}{6} = \dfrac{{\widehat C}}{7} = \dfrac{{\widehat A + \widehat B + \widehat C}}{{5 + 6 + 7}} = \dfrac{{180^\circ }}{{18}} = 10^\circ \\ \Rightarrow \widehat A = 10^\circ .5 = 50^\circ \\\widehat B = 10^\circ .6 = 60^\circ \\\widehat C = 10^\circ .7 = 70^\circ \end{array}\)
Vậy số đo 3 góc \(\widehat A,\widehat B,\widehat C\) lần lượt là \(50^\circ ;60^\circ ;70^\circ \)

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
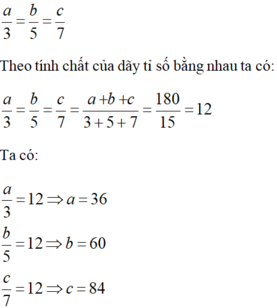
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o
Áp dụng t/c dtsbn:
\(\dfrac{\widehat{A}}{5}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{5+2+3}=\dfrac{180^0}{10}=18^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=90^0\\\widehat{B}=36^0\\\widehat{C}=54^0\end{matrix}\right.\)
Do đó tg ABC vuông tại A
Xét tg AHB vuông tại H có \(\widehat{BAH}+\widehat{B}=90^0\Rightarrow\widehat{BAH}=90^0-36^0=54^0\)
Gọi số đo ba góc A, B, C lần lượt là: x, y, z
Theo đề ta có: x/5 = y/2 = z/3, x + y + z= 180 độ
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
x/5 + y/2 + z/3 = (x+y+z)/(5+2+3)= 180/10=18
=> y/2=18=>y=18.2=36
Vì H là đường cao của tam giác ABC nên góc BHA=90 độ
Ta lại có: góc B + góc BAH + góc BHA= 180 độ
hay 36 độ + 90 độ + góc BHA= 180 độ
=> 126 độ + góc BHA= 180 độ
=> góc BHA= 180 độ - 126 độ = 54 độ
Vậy góc BHA có số đo là 54 độ