Cho tam giác đều ABC. Trên các cạnh AB, AC lần lượt lấy các điểm D, E sao cho AD = AE. Gọi G là trọng tâm tam giác ADE và M là trung điểm BE. Tính số đo các góc của tam giác GMC.
Giúp mik với !!! Mik đng cần gấp !!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 10 2017
Trên tia đối của KG lấy điểm F sao cho KG=KF.
Ta có: \(\Delta\)ABC đều => ^A=600. Xét \(\Delta\)ADE có: ^A=600, AD=AE
=> \(\Delta\)ADE đều. Mà G là trọng tâm của \(\Delta\)ADE
=> G cũng là giao của 3 đường trung trực trong \(\Delta\)ABC
=> DG=AG (T/c đường trung trực) (1)
Xét \(\Delta\)GDK và \(\Delta\)FCK:
KD=KC
^DKG=^CKF => \(\Delta\)GDK=\(\Delta\)FCK (c.g.c)
KG=KF
=> DG=CF (2 cạnh tương ứng). (2)
Từ (1) và (2) => AG=CF.
Cũng suy ra đc: ^GDK=^FCK (2 góc tương ứng) => ^GDE+^EDK=^FCB+^BCK
Lại có: ED//BC (Vì \(\Delta\)ADE đều) => ^EDK=^BCK (So le trong)
=> ^GDE=^FCB (Bớt 2 vế cho ^EDK, ^BCK) (3)
Xét \(\Delta\)ADE: Đều, G trọng tâm => DG cũng là phân giác ^ADE
=> ^GDE=^ADE/2=300.
Tương tự tính được: ^GAD=300 => ^GDE=^GAD hay ^GDE=^GAB (4)
Từ (3) và (4) => ^GAB=^FCB
Xét \(\Delta\)AGB và \(\Delta\)CFB có:
AB=CB
^GAB=^CFB => \(\Delta\)AGB=\(\Delta\)CFB (c.g.c)
AG=CF
=> GB=FB (2 cạnh tương ứng) (5).
=> ^ABG=^CBF (2 góc tương ứng). Lại có:
^ABG+^GBC=^ABC=600. Thay ^ABG=^CBF ta thu được:
^CBF+^GBC=600 => ^GBF=600 (6)
Từ (5) và (6) => \(\Delta\)GBF là tam giác đều. => ^BGF=600 hay ^BGK=600
K là trung điểm của GF => BK là phân giác ^GBF => ^GBK= ^GBF/2=300
Xét \(\Delta\)BGK: ^BGK=600, ^GBK=300 => ^BKG=900.
ĐS: ^GBK=300, ^BGK=600, ^BKG=900.
*Xong*
26 tháng 2 2022
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: Ta có: ΔABC=ΔADE
nên BC=DE(1)
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=BC/2(2)
Ta có: ΔADE vuông tại A
mà AN là đường trung tuyến
nên AN=DE/2(3)
Từ (1), (2) và (3) suy ra AM=AN
30 tháng 1 2020
Một đội xe tải trong 3 ngày phải chuyển hết một số hàng hóa 2 ngày đầu độc chất thải đã chuyển được 13,14 số hàng hóa biết rằng ngày thứ hai đội chuyển được 3/7 số hàng hóa vận chuyển ít hơn ngày thứ nhất 30 tấn hỏi ngày thứ ba đôi chân bao nhiêu hàng hóa
GS
30 tháng 1 2020
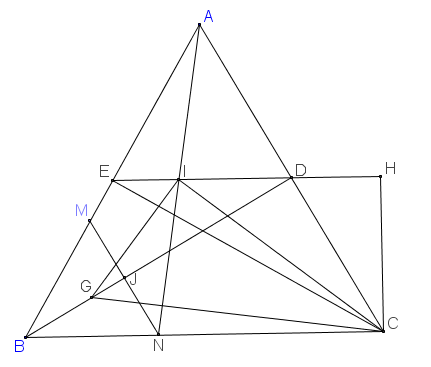
Gọi E, D lần lượt là trung điểm AB, AC, ta có I, E, D thẳng hàng
MN cắt BD tại J, hạ CH vuông góc ED tại H
Có DH=DC2=ED2DH=DC2=ED2
=>EDEH=23EDEH=23
Có BGBD=BGBJ.BJBDBGBD=BGBJ.BJBD
=23.BNBC=EDEH.EIED=23.BNBC=EDEH.EIED
=>BGBD=EIEHBGBD=EIEH
<=>BGEI=BDEHBGEI=BDEH (1)
Ta có △CBD∼△CEH△CBD∼△CEH (g, g)
=>CBCE=BDEH=BGEICBCE=BDEH=BGEI
=>△CBG∼△CEI△CBG∼△CEI (c, g, c) (2)
(2) =>ˆBCG=ˆECIBCG^=ECI^
<=>ˆBCG+ˆGCE=ˆGCE+ˆECIBCG^+GCE^=GCE^+ECI^
<=>ˆBCE=ˆGCIBCE^=GCI^ (3)
(2) =>BCEC=GCICBCEC=GCIC (4)
từ (3, 4) =>△BEC∼△GIC△BEC∼△GIC (c, g, c)
=>ˆI=90∘I^=90∘, ˆG=60∘G^=60∘ (đpcm)
Hình gửi kèm
14 tháng 1 2018
Vẽ H sao cho I là trung điểm GH rồi chứng minh rằng tam giác GHB là tam giác đều bằng cách chứng minh tam giác HCB =tam giác GAB(c.g.c)
Bạn tham khảo nhé:
Trên tia đối của KG lấy điểm F sao cho KG=KF.
Ta có: ΔABC đều => ^A=600. Xét ΔADE có: ^A=600, AD=AE
=> ΔADE đều. Mà G là trọng tâm của ΔADE
=> G cũng là giao của 3 đường trung trực trong ΔABC
=> DG=AG (T/c đường trung trực) (1)
Xét ΔGDK và ΔFCK:
KD=KC
^DKG=^CKF => ΔGDK=ΔFCK (c.g.c)
KG=KF
=> DG=CF (2 cạnh tương ứng). (2)
Từ (1) và (2) => AG=CF.
Cũng suy ra đc: ^GDK=^FCK (2 góc tương ứng) => ^GDE+^EDK=^FCB+^BCK
Lại có: ED//BC (Vì ΔADE đều) => ^EDK=^BCK (So le trong)
=> ^GDE=^FCB (Bớt 2 vế cho ^EDK, ^BCK) (3)
Xét ΔΔADE: Đều, G trọng tâm => DG cũng là phân giác ^ADE
=> ^GDE=^ADE/2=300.
Tương tự tính được: ^GAD=300 => ^GDE=^GAD hay ^GDE=^GAB (4)
Từ (3) và (4) => ^GAB=^FCB
Xét ΔAGB và ΔCFB có:
AB=CB
^GAB=^CFB => ΔAGB=ΔCFB (c.g.c)
AG=CF
=> GB=FB (2 cạnh tương ứng) (5).
=> ^ABG=^CBF (2 góc tương ứng). Lại có:
^ABG+^GBC=^ABC=600. Thay ^ABG=^CBF ta thu được:
^CBF+^GBC=600 => ^GBF=600 (6)
Từ (5) và (6) => ΔGBF là tam giác đều. => ^BGF=600 hay ^BGK=600
K là trung điểm của GF => BK là phân giác ^GBF => ^GBK= ^GBF/2=300
Xét ΔBGK: ^BGK=600, ^GBK=300 => ^BKG=900.
ĐS: ^GBK=300, ^BGK=600, ^BKG=900.