Cho tam giác cân ABC (AB = AC) nội tiếp trong đường tròn (0).Qua A vẽ một đường thẳng cắt cạnh BC ở D và cắt đường tròn (0) tại E. Chứng minh rằng AB² = AD.AE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 4 2023
a: góc BAC=góc BCA
=>sđ cung BC=sđ cung BA
b: xy//DE
=>góc AED=góc yAE=góc ABC
c: góc AED=góc ABC
=>góc ABC+góc DEC=180 độ
=>BCDE nội tiếp
CM
3 tháng 4 2019
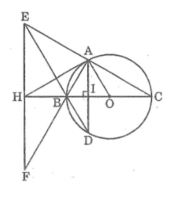
Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên: HA = HE = HF = (1/2).EF (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.
CM
6 tháng 10 2017
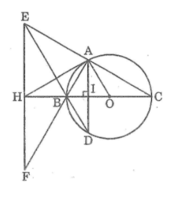
Gọi I là giao điểm của AD và BC
Vì BC là đường trung trực của AD nên theo tính chất đường trung trực ta có:
BA = BD
Tam giác BAD cân tại B có BI ⊥ AD nên BI là tia phân giác của góc ABD
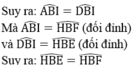
Tam giác EBF có BH là tia phân giác của góc EBF và BH ⊥ EF nên tam giác EBF cân tại B.
AT
23 tháng 6 2021
a) Vì MA là tiếp tuyến \(\Rightarrow\angle MAB=\angle MCA\) (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
Xét \(\Delta MAB\) và \(\Delta MCA:\) Ta có: \(\left\{{}\begin{matrix}\angle MAB=\angle MCA\\\angle AMCchung\end{matrix}\right.\)
\(\Rightarrow\Delta MAB\sim\Delta MCA\left(g-g\right)\Rightarrow\dfrac{MA}{MC}=\dfrac{MB}{MA}\Rightarrow MA^2=MB.MC\)
b) Vì \(DE\parallel AM\) và \(AM\bot AO\) (tiếp tuyến) \(\Rightarrow DE\bot AO\)
\(\Rightarrow\angle OAD+\angle ADE=90\)
Ta có: \(\angle OAD=\dfrac{180-\angle AOC}{2}\) (\(\Delta OAC\) cân tại O) \(=90-\dfrac{1}{2}\angle AOC\)
\(=90-\angle ABC\)
\(\Rightarrow\angle ADE=\angle ABC\Rightarrow BCDE\) nội tiếp \(\Rightarrow\angle BEC=\angle BDC=90\)
\(\Rightarrow\) CE là đường cao
c) Vì N là điểm chính giữa cung BC \(\Rightarrow\angle BAN=\angle CAN\)
\(\Rightarrow AN\) là phân giác
Ta có: AI là phân giác \(\angle BAD\Rightarrow\dfrac{IB}{ID}=\dfrac{AB}{AD}\left(1\right)\)
AK là phân giác \(\angle CAE\Rightarrow\dfrac{KC}{KE}=\dfrac{AC}{AE}\left(2\right)\)
Xét \(\Delta DAB\) và \(\Delta EAC:\) Ta có: \(\left\{{}\begin{matrix}\angle AEC=\angle ADB=90\\\angle BACchung\end{matrix}\right.\)
\(\Rightarrow\Delta DAB\sim\Delta EAC\left(g-g\right)\Rightarrow\dfrac{AB}{AD}=\dfrac{AC}{AE}\left(3\right)\)
Từ (1),(2) và (3) \(\Rightarrow\dfrac{IB}{ID}=\dfrac{KC}{KE}\)
Theo đề: \(\dfrac{IB}{ID}.\dfrac{KC}{KE}=\dfrac{IB}{ID}+\dfrac{KC}{KE}\Rightarrow\left(\dfrac{AB}{AD}\right)^2=2\dfrac{AB}{AD}\Rightarrow\dfrac{AB}{AD}=2\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{1}{2}\Rightarrow cosBAC=\dfrac{1}{2}\Rightarrow\angle BAC=60\)
Vậy tam giác ABC có \(\angle BAC=60\) thì \(\dfrac{IB}{ID}.\dfrac{KC}{KE}=\dfrac{IB}{ID}+\dfrac{KC}{KE}\)
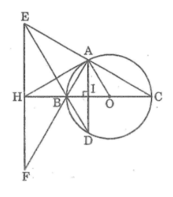
Xét ΔADB và ΔABE có
\(\widehat{BAD}\) chung
\(\widehat{ABD}=\widehat{AEB}\)
Do đó: ΔADB\(\sim\)ΔABE
Suy ra: \(\dfrac{AD}{AB}=\dfrac{AB}{AE}\)
hay \(AB^2=AD\cdot AE\)