BÀI 9 THU GỌN CÁC ĐƠN THỨC ĐỒNG DẠNG
23*X3*Y3+17*X3*Y3+(-50X3)*Y3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a, x^3 + y^3 + x + y`
`= (x+y)(x^2-xy+y^2)+x+y`
`= (x+y)(x^2-xy+y^2+1)`
`b, x^3 - y^3 + x -y`
`= (x-y)(x^2+xy+y^2)+x-y`
`= (x-y)(x^2+xy+y^2+1)`
`c, (x-y)^3 + (x+y)^3`
`= (x-y+x+y)(x^2-2xy+y^2 - x^2 + y^2 + x^2 + 2xy + y^2)`
`= (2x)(x^2 + 3y^2)`
`d, x^3 - 3x^2y + 3xy^2 - y^3 + y^2 - x^2`
`= (x-y)^3 + (y-x)(x+y)`
`=(x-y)(x^2+2xy+y^2-x-y)`
a: =(x+y)(x^2-xy+y^2)+(x+y)
=(x+y)(x^2-xy+y^2+1)
b: =(x-y)(x^2+xy+y^2)+(x-y)
=(x-y)(x^2+xy+y^2+1)
c: =x^3-3x^2y+3xy^2-y^3+x^3+3x^2y+3xy^2-y^3
=2x^3+6xy^2
d: =(x-y)^3+(y-x)(y+x)
=(x-y)[(x-y)^2-(x+y)]

Q = x - y 3 + y + x 3 + y - x 3 – 3xy(x + y)
= x 3 – 3 x 2 y + 3x y 2 – y 3 + y 3 + 3 y 2 .x + 3y x 2 + x 3 + y 3 – 3 y 2 .x +3y x 2 – x 3 – 3 x 2 y – 3x y 2
= x 3 – 3 x 2 y + 3x y 2 – y 3 + y 3 + 3.x y 2 + 3 x 2 .y + x 3 + y 3 – 3x. y 2 + 3 x 2 .y – x 3 – 3 x 2 y – 3x y 2
= ( x 3 + x 3 – x 3 )+ ( - 3 x 2 y + 3 x 2 y+ 3 x 2 y – 3 x 2 y)+ (3x y 2 + 3x y 2 - 3x y 2 - 3x y 2 ) + (- y 3 + y 3 + y 3 )
= x 3 + 0 x 2 y + 0.x y 2 + y 3
= x 3 + y 3

\(a,x+y=1\Leftrightarrow\left(x+y\right)^3=1\Leftrightarrow x^3+y^3+3xy\left(x+y\right)=1\\ \Leftrightarrow x^3+y^3+3xy\cdot1=1\Leftrightarrow x^3+y^3+3xy=1\)
\(b,x^3-y^3-3xy\\ =x^3-3x^2y+3xy^2-y^3-3xy+3x^2y-3xy^2\\ =\left(x-y\right)^3-3xy\left(x-y-1\right)\\ =1^3-3xy\left(1-1\right)=1-0=1\)
\(c,x^3+y^3+3xy\left(x^2+y^2\right)+6x^2y^2\left(x+y\right)\\ =\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\left[\left(x+y\right)^2-2xy\right]+6x^2y^2\\ =x^2-xy+y^2+3xy-6x^2y^2+6x^2y^2\\ =x^2+2xy+y^2=\left(x+y\right)^2=1\)

\(a,=\left(3+x\right)\left(9-3x+x^2\right)\\ b,=\left(4x+0,1\right)\left(16x^2-0,4x+0,01\right)\\ c,=\left(2-3x\right)\left(4+6x+9x^2\right)\\ d,=\left(\dfrac{x}{5}-\dfrac{y}{3}\right)\left(\dfrac{x^2}{25}+\dfrac{xy}{15}+\dfrac{y^2}{9}\right)\)

10: \(x\left(x-y\right)+x^2-y^2\)
\(=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x+x+y\right)\)
\(=\left(x-y\right)\left(2x+y\right)\)
11: \(x^2-y^2+10x-10y\)
\(=\left(x^2-y^2\right)+\left(10x-10y\right)\)
\(=\left(x-y\right)\left(x+y\right)+10\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y+10\right)\)
12: \(x^2-y^2+20x+20y\)
\(=\left(x^2-y^2\right)+\left(20x+20y\right)\)
\(=\left(x-y\right)\left(x+y\right)+20\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y+20\right)\)
13: \(4x^2-9y^2-4x-6y\)
\(=\left(4x^2-9y^2\right)-\left(4x+6y\right)\)
\(=\left(2x-3y\right)\left(2x+3y\right)-2\left(2x+3y\right)\)
\(=\left(2x+3y\right)\left(2x-3y-2\right)\)
14: \(x^3-y^3+7x^2-7y^2\)
\(=\left(x^3-y^3\right)+\left(7x^2-7y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\cdot\left(x^2-y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+7x+7y\right)\)
15: \(x^3+4x-\left(y^3+4y\right)\)
\(=x^3-y^3+4x-4y\)
\(=\left(x^3-y^3\right)+\left(4x-4y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+4\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+4\right)\)
16: \(x^3+y^3+2x+2y\)
\(=\left(x^3+y^3\right)+\left(2x+2y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+2\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2+2\right)\)
17: \(x^3-y^3-2x^2y+2xy^2\)
\(=\left(x^3-y^3\right)-\left(2x^2y-2xy^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-2xy\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-2xy\right)\)
\(=\left(x-y\right)\left(x^2-xy+y^2\right)\)
18: \(x^3-4x^2+4x-xy^2\)
\(=x\left(x^2-4x+4-y^2\right)\)
\(=x\left[\left(x^2-4x+4\right)-y^2\right]\)
\(=x\left[\left(x-2\right)^2-y^2\right]\)
\(=x\left(x-2-y\right)\left(x-2+y\right)\)

a: \(A=2x^3y^2\left(-\dfrac{1}{4}x^2y\right)\)
\(=2\cdot\dfrac{-1}{4}\cdot x^3\cdot x^2\cdot y^2\cdot y\)
\(=-\dfrac{1}{2}x^5y^3\)
Bậc là 5+3=8
b: \(A+B=-\dfrac{1}{2}x^5y^3+\dfrac{-3}{2}x^3y^3\)
c: Thay x=-1 và y=2 vào A, ta được:
\(A=-\dfrac{1}{2}\cdot\left(-1\right)^5\cdot2^3=\dfrac{1}{2}\cdot8=4\)

Đáp án đúng là (A) 3x2 y3 và 3x3 y2 là hai đơn thức đồng dạng.

M = x 3 + y 3 + z 3 - 3 x y z x 2 + y 2 + z 2 - x y - y z - x z
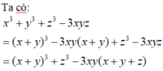
![]()
![]()
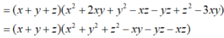
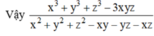
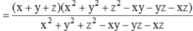
![]()

a) \(A=x^3+y^3+3xy\)
\(=x^3+y^3+3xy\left(x+y\right)\) (do \(x+y=1\))
\(=x^3+3x^2y+3xy^2+y^3\)
\(=\left(x+y\right)^3\) \(=1\)
b) \(B=x^3-y^3-3xy\)
\(=x^3-y^3-3xy\left(x-y\right)\) (do \(x-y=1\))
\(=x^3-3x^2y+3xy^2-y^3\)
\(=\left(x-y\right)^3\) \(=1\)
\(-10x^3y^3\)
ghi các bước giải ra bạn ei