Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(Lưu ý: ΔABC vuông tại A nên ∠ B + ∠ C = 90 °
Giải tam giác tức là đi tìm số đo các cạnh và các góc còn lại.)
a)
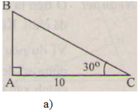
∠ B = 90 o - ∠ C = 90 ° - 30 ° = 60 °
c = b . t g C = 10 . t g 30 ° ≈ 5 , 77 ( c m )
![]()
b)
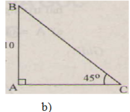
∠ B = 90 ° - ∠ C = 90 ° - 45 ° = 45 °
=> ΔABC cân => b = c = 10 (cm)
![]()
c)
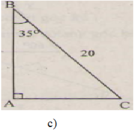
∠ B = 90 o - ∠ C = 90 ° - 35 ° = 55 ° b = a sin B = 20 . sin 35 ° ≈ 11 , 47 ( c m ) c = a sin C = 20 . sin 55 ° ≈ 16 , 38 ( c m )
d)
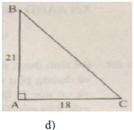
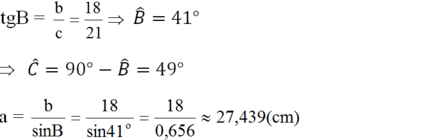
(Ghi chú: Bạn nên sử dụng các kí hiệu cạnh là a, b, c (thay vì BC, AC, AB) để đồng bộ với đề bài đã cho.
Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.
hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))

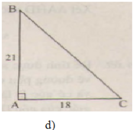
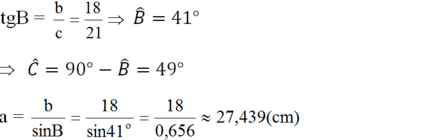
(Ghi chú: Bạn nên sử dụng các kí hiệu cạnh là a, b, c (thay vì BC, AC, AB) để đồng bộ với đề bài đã cho.
Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.
hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))

Áp dụng định lí Pytago vào ΔDEF vuông tại E, ta có
\(DF^2=DE^2+EF^2\)
\(\Leftrightarrow DF^2=21^2+18^2=765\)
\(\Leftrightarrow DF=\sqrt{765}=3\sqrt{85}cm\)
Xét ΔDEF vuông tại E có
\(\sin\widehat{D}=\frac{EF}{DF}=\frac{18}{3\sqrt{85}}=\frac{6}{\sqrt{85}}\)
\(\Rightarrow\widehat{D}\simeq40^036'\)
Ta có: ΔDEF vuông tại E(gt)
\(\Rightarrow\widehat{D}+\widehat{F}=90^0\)(hai góc nhọn phụ nhau)
\(\Rightarrow\widehat{F}=90^0-\widehat{D}=90^0-40^036'=49^024'\)
Vậy: \(DF=3\sqrt{85}cm\); \(\widehat{D}\simeq40^036'\); \(\widehat{F}=49^024'\)

a: góc C=90-40=50 độ
sin C=AB/BC
=>7/BC=sin50
=>BC=9,14(cm)
=>\(AC\simeq5,88\left(cm\right)\)
b: góc B=90-30=60 độ
sin C=AB/BC
=>AB/16=1/2
=>AB=8cm
=>AC=8*căn 3(cm)
c: BC=căn 18^2+21^2=3*căn 85(cm)
tan C=AB/AC=6/7
=>góc C=41 độ
=>góc B=49 độ
d: AB=căn 13^2-12^2=5cm
sin C=AB/BC=5/13
=>góc C=23 độ
=>góc B=67 độ

4:
\(cos75=sin15;cos18=sin72\)
\(15< 65< 70< 72\)
=>\(sin15< sin65< sin70< sin72\)
=>\(cos75< sin65< sin70< cos18\)
5:
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=BC/2=6cm
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2+6^2=10^2\)
=>HA2=64
=>HA=8(cm)
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot8\cdot12=4\cdot12=48\left(cm^2\right)\)
b: Xét ΔAHB vuông tại H có
\(sinB=\dfrac{AH}{AB}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
=>\(\widehat{C}\simeq53^0\)