Trong một kỳ thi mỗi sinh viên phải thi 2 môn. Một sinh viên A ước lượng rằng: Xác suất đạt môn thứ nhất là 0,8; Nếu đạt môn thứ nhất thì xác suất đạt môn thứ hai là 0,6; Nếu không đạt môn thứ nhất thì xác suất đạt một thứ hai là 0,3.
a) Xác suất để sinh viên A đạt môn thứ hai là?
b) Xác suất để sinh viên A đạt ít nhất 1 môn là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

10 tháng 9 2021
a) Xác suất để có 2 sinh viên thi đậu:
\(0,6.0,7.0,2+0,6.0,3.0,8+0,4.0,7.0,8=0,452\)
b) Xác suất để có 2 sinh viên thi đậu trong đó sinh viên II không thi đậu:
\(0,6.0,3.0,8=0,144\)

9 tháng 6 2016
Không gian mẫu : " Chọn 5 học sinh bất kì để đăng kí dự thi " là C530 cách
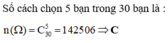
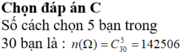
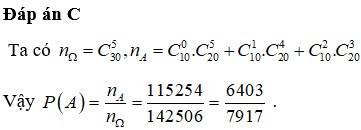
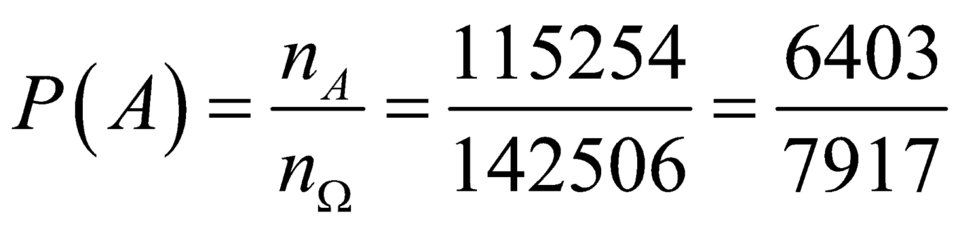
Gọi \(B_1\) là biến cố "sinh viên A đạt môn thứ nhất"
\(B_2\) là biến cố "sinh viên A đạt môn thứ hai"
\(\Rightarrow P\left(B_1\right)=0,8\) ; \(P\left(B_2|B_1\right)=0,6\) ; \(P\left(B_2|\overline{B_1}\right)=0,3\)
a/ Xác suất đạt môn thứ hai:
\(P\left(B_2\right)=P\left(B_1\right).P\left(B_2|B_1\right)+P\left(\overline{B_1}\right)P\left(B_2|\overline{B_1}\right)\)
\(=0,8.0,6+0,2.0,3=0,54\)
b/ Xác suất để đạt ít nhất 1 môn:
\(P\left(B_1\cup B_2\right)=P\left(B_1\right)+P\left(B_2\right)-P\left(B_1B_2\right)\)
\(=P\left(B_1\right)+P\left(B_2\right)-P\left(B_1\right)P\left(B_2|B_1\right)=0,86\)