Cho hàm số: y =f(x)=x.
Tính: f(0);f(1);f(-1);f(3);f(-3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1 : làm tương tự với bài 2;3 nhé
Ta có : \(f\left(0\right)=c=2010;f\left(1\right)=a+b+c=2011\)
\(\Rightarrow f\left(1\right)=a+b=1\)
\(f\left(-1\right)=a-b+c=2012\Rightarrow f\left(-1\right)=a-b=2\)
\(\Rightarrow a+b=1;a-b=2\Rightarrow2a=3\Leftrightarrow a=\dfrac{3}{2};b=\dfrac{3}{2}-2=-\dfrac{1}{2}\)
Vậy \(f\left(-2\right)=4a-2b+c=\dfrac{4.3}{2}-2\left(-\dfrac{1}{2}\right)+2010=6+1+2010=2017\)

Chọn C.
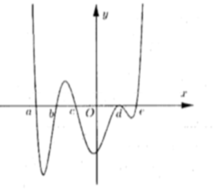
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
Bài 2:
Lần lượt thay các giá trị của x, ta có:
_Y=f(-2)=-2.(-2)+3=7
_Y=f(-1)=-2.(-1)+3=1
_Y=f(0)=-2.0+3=3
_Y=f(-1/2)=-2.(-1/2)+3=4
_Y=f(1/2)=-2.1/2+3=2

1.
y=f(-1)=3*(-1)-2=-5
y=f(0)=3*0-2=-2
y=f(-2)=3*(-2)-2=-8
y=f(3)=3*3-2=7
Câu 2,3a làm tương tự,chỉ việc thay f(x) thôi.
3b
Khi y=5 =>5=5-2*x=>2*x=0=> x=0
Khi y=3=>3=5-2*x=>2*x=2=>x=1
Khi y=-1=>-1=5-2*x=>2*x=6=>x=3
f(-1)=3.1-2=3-2=1
f(0)=3.0-2=0-2=-2
f(-2)=3.(-2)-2=-6-2=-8
f(3)=3.3-2=9-2=7

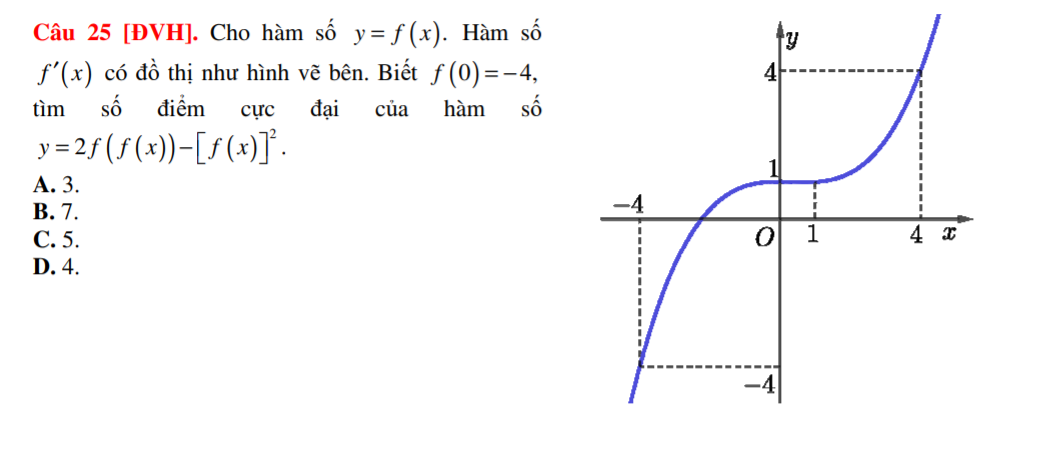
\(y'=2f'\left(x\right).f'\left(f\left(x\right)\right)-2f'\left(x\right).f\left(x\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f'\left(f\left(x\right)\right)=f\left(x\right)\end{matrix}\right.\)
Từ đồ thị ta có \(f'\left(x\right)=0\Rightarrow x=x_1\) với \(-4< x_1< 0\)
Xét phương trình \(f'\left(f\left(x\right)\right)=f\left(x\right)\), đặt \(f\left(x\right)=t\Rightarrow f'\left(t\right)=t\)
Vẽ đường thẳng \(y=t\) (màu đỏ) lên cùng đồ thị \(y=f'\left(t\right)\) như hình vẽ:
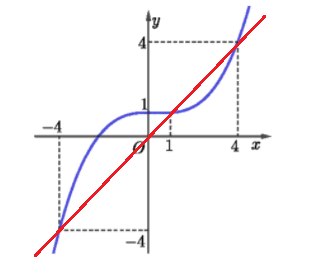
Ta thấy 2 đồ thị cắt nhau tại 3 điểm: \(t=\left\{-4;1;4\right\}\)
\(\Rightarrow\left[{}\begin{matrix}f\left(x\right)=-4\\f\left(x\right)=1\\f\left(x\right)=4\end{matrix}\right.\) (1)
Mặt khác từ đồ thị \(f'\left(x\right)\) và \(f\left(0\right)=-4\) ta được BBT của \(f\left(x\right)\) có dạng:
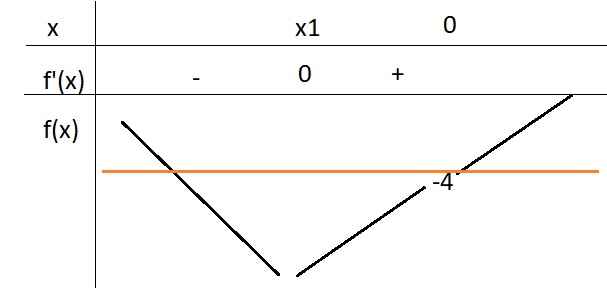
Từ đó ta thấy các đường thẳng \(y=k\ge-4\) luôn cắt \(y=f\left(x\right)\) tại 2 điểm phân biệt
\(\Rightarrow\) Hệ (1) có 6 nghiệm phân biệt (trong đó 3 nghiệm nhỏ hơn \(x_1\) và 3 nghiệm lớn hơn \(x_1\))
Từ đó ta có dấu của y' như sau:

Có 3 lần y' đổi dấu từ dương sang âm nên hàm có 3 cực đại

Chọn D
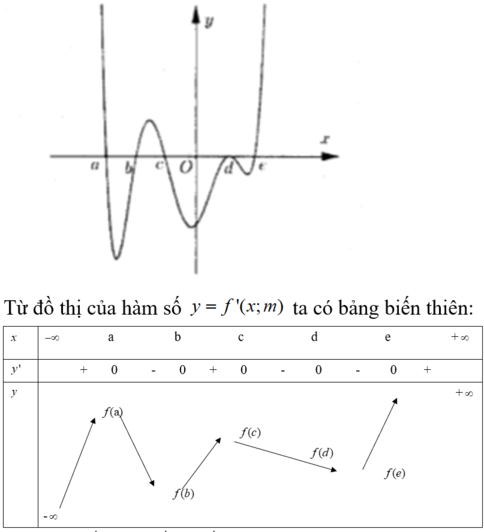
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
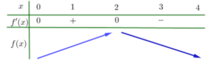
Từ bảng biến thiên, ta có nhận xét sau: ![]()
![]()
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
![]()
![]()


y =f(0)=0
y =f(1)=1
y =f(-1)=-1
y =f(3)=3
y =f(-3)=-3
Cho hàm số: y =f(x)=x.
Tính: f(0);f(1);f(-1);f(3);f(-3)
Giải
Ta thay f(0);f(1);f(-1);f(3);f(-3) vào f(x)=x ,ta đc:
f(0)=0
f(1)=1
f(-1)=-1
f(3)=3
f(-3)=-3