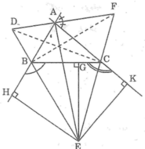
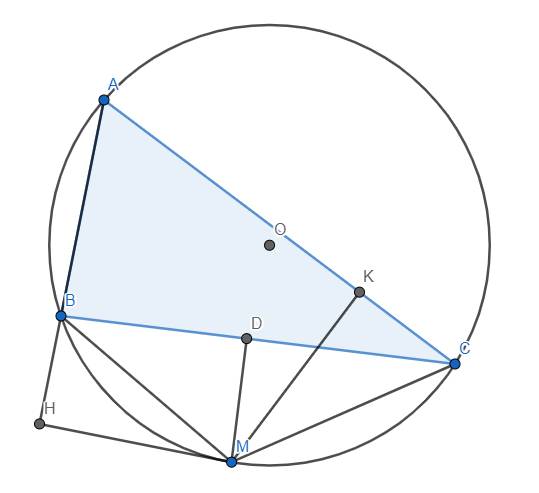
Cho tam giác ABC . Gọi H là chân đường cao kẻ từ A, biết rằng H nằm trên đoạn thẳng BC và không trùng khớp vói B hoặc C. Đường thẳng AB cắt đường tròn ngoài tiếp tam giác ACH tại D phân biệt với A. Đường thẳng AC cắt đường tròn ngoại tiếp tam giác ABH tại E phân biệt với A.
1) Gọi I, J lần lượt là trung điểm của AB và AC. Chứng minh rằng bốn điểm I, J, D, E cùng nằm trên một đường tròn.
2) Chứng minh rằng HA là tia phân giác của góc EHD.
3) Xác định mối liên hệ giữa AB, AC và AH để DE tiếp xúc với cả hai đường tròn nói trên.