cho hàm số y = f(x) = x3+ x . Tính f(1) , f(-1) ,f(2) , f( -2) ; f(3);f(-3)và so sánh f(a) với f(-a)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
1a.
\(y'=3x^2.f'\left(x^3\right)-2x.g'\left(x^2\right)\)
b.
\(y'=\dfrac{3f^2\left(x\right).f'\left(x\right)+3g^2\left(x\right).g'\left(x\right)}{2\sqrt{f^3\left(x\right)+g^3\left(x\right)}}\)
2.
\(f'\left(x\right)=\left(m-1\right)x^3+\left(m-2\right)x^2-2mx+3=0\)
Để ý rằng tổng hệ số của vế trái bằng 1 nên pt luôn có nghiệm \(x=1\), sử dụng lược đồ Hooc-ne ta phân tích được:
\(\Leftrightarrow\left(x-1\right)\left[\left(m-1\right)x^2+\left(2m-3\right)x-3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(m-1\right)x^2+\left(2m-3\right)x-3=0\left(1\right)\end{matrix}\right.\)
Xét (1), với \(m=1\Rightarrow x=-3\)
- Với \(m\ne1\Rightarrow\Delta=\left(2m-3\right)^2+12\left(m-1\right)=4m^2-3\)
Nếu \(\left|m\right|< \dfrac{\sqrt{3}}{2}\Rightarrow\) (1) vô nghiệm \(\Rightarrow f'\left(x\right)=0\) có đúng 1 nghiệm
Nếu \(\left|m\right|>\dfrac{\sqrt{3}}{2}\Rightarrow\left(1\right)\) có 2 nghiệm \(\Rightarrow f'\left(x\right)=0\) có 3 nghiệm
6 tháng 12 2021
Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
6 tháng 12 2021
Bài 2:
Lần lượt thay các giá trị của x, ta có:
_Y=f(-2)=-2.(-2)+3=7
_Y=f(-1)=-2.(-1)+3=1
_Y=f(0)=-2.0+3=3
_Y=f(-1/2)=-2.(-1/2)+3=4
_Y=f(1/2)=-2.1/2+3=2
ND
0
ND
0
CM
23 tháng 12 2017
Đáp án D.
Ta có thể lập bảng xét dấu của f'(x) tuy nhiên thì ta có thể dùng mẹo như sau. Tại x=0; x=-2 thì y' đổi dấu do có mũ la lẻ còn x=1 thì không đổi dấu do mũ là chẵn. Vì vậy ta có thể có 2 cực trị.
6 tháng 12 2016
1.
y=f(-1)=3*(-1)-2=-5
y=f(0)=3*0-2=-2
y=f(-2)=3*(-2)-2=-8
y=f(3)=3*3-2=7
Câu 2,3a làm tương tự,chỉ việc thay f(x) thôi.
3b
Khi y=5 =>5=5-2*x=>2*x=0=> x=0
Khi y=3=>3=5-2*x=>2*x=2=>x=1
Khi y=-1=>-1=5-2*x=>2*x=6=>x=3
14 tháng 12 2016
f(-1)=3.1-2=3-2=1
f(0)=3.0-2=0-2=-2
f(-2)=3.(-2)-2=-6-2=-8
f(3)=3.3-2=9-2=7
AH
Akai Haruma
Giáo viên
8 tháng 10 2021
Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.
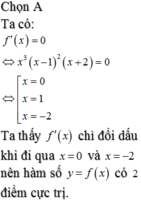
*Tính F(1)
Thay x=1 vào hàm số \(y=f\left(x\right)=x^3+x\), ta được
\(F\left(1\right)=1^3+1=2\)
Vậy: Khi x=1 thì giá trị của hàm số \(y=f\left(x\right)=x^3+x\) là 2
*Tính F(-1)
Thay x=-1 vào hàm số \(y=f\left(x\right)=x^3+x\), ta được
\(F\left(-1\right)=\left(-1\right)^3+\left(-1\right)=-1-1=-2\)
Vậy: Khi x=-1 thì giá trị của hàm số \(y=f\left(x\right)=x^3+x\) là -2
*Tính F(2)
Thay x=2 vào hàm số \(y=f\left(x\right)=x^3+x\), ta được
\(F\left(2\right)=2^3+2=10\)
Vậy: Khi x=2 thì giá trị của hàm số \(y=f\left(x\right)=x^3+x\) là 10
*Tính F(-2)
Thay x=-2 vào hàm số \(y=f\left(x\right)=x^3+x\), ta được
\(F\left(-2\right)=\left(-2\right)^3+\left(-2\right)=-8-2=-10\)
Vậy: Khi x=-2 thì giá trị của hàm số \(y=f\left(x\right)=x^3+x\) là -10
*Tính F(3)
Thay x=3 vào hàm số \(y=f\left(x\right)=x^3+x\), ta được
\(F\left(3\right)=3^3+3=27+3=30\)
Vậy: Khi x=3 thì giá trị của hàm số \(y=f\left(x\right)=x^3+x\) là 30
*Tính F(-3)
Thay x=-3 vào hàm số \(y=f\left(x\right)=x^3+x\), ta được
\(F\left(-3\right)=\left(-3\right)^3+\left(-3\right)=-27-3=-30\)
Vậy: Khi x=-3 thì giá trị của hàm số \(y=f\left(x\right)=x^3+x\) là -30
*So sánh F(a) và F(-a)
Nhận thấy khi thay a và -a vào thì giá trị đều là hai số đối nhau
hay F(a)=-F(-a)