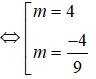Giải x^4-10x^2+2m^2+7m=0 có 4 nghiệm lập thành cấp số cộng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 1 2021
Câu 1: Gọi 3 số là a;b;c
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=6\\2b=a+c\\a^2+b^2+c^2=30\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\a+c=4\\a^2+c^2=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}b=2\\c=4-a\\a^2+\left(4-a\right)^2=26\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\c=5\\a=-1\end{matrix}\right.\left(\text{V\text{ì} }a< c\right)\)
2 tháng 1 2021
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)
29 tháng 11 2019
Đặt t = x2.
Khi đó ta có phương trình: t2 – 10t + 2m2 + 7m = 0.
Phương trình đã cho có nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
+ Với điều kiện trên thì phương trình (*) có hai nghiệm dương phân biệt là t1, t2(t1 < t2).
Khi đó phương trình đã cho có bốn nghiệm phân biệt là :
Bốn nghiệm này lập thành một cấp số cộng khi
Theo định lý Vi-ét ta có: t1 + t2 = 10 ; t1.t2 = 2m2 + 7m.
⇒ Ta có hệ phương trình:
Cả hai giá trị này đều thỏa mãn điều kiện nên đều có thể nhận được.
Do đó:
CM
16 tháng 4 2017
Chọn B.
Đặt t = x2, t ≥ 0.
Phương trình trở thành: t2 – 2(m + 1)t + 2m + 1 = 0 (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi PT (2) có hai nghiệm dương phân biệt t2 > t1 > 0.
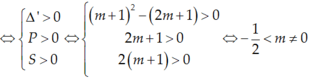
Khi đó PT(2) có bốn nghiệm là: 
Bốn nghiệm này lập thành cấp số cộng khi :
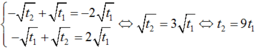
Theo định lý viet thì :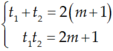 
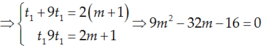
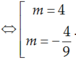
Vậy m = 4 hoặc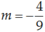 
là những giá trị cần tìm.
CM
28 tháng 2 2018
Chọn B
Đặt t = x 2 , t ≥ 0 .
Phương trình trở thành: t 2 − 2 m + 1 t + 2 m + 1 = 0 (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi PT (2) có hai nghiệm dương phân biệt t2 > t1 > 0 .
Δ ' > 0 P > 0 S > 0
⇔ m + 1 2 − 2 m + 1 > 0 2 m + 1 > 0 2 m + 1 > 0 ⇔ − 1 2 < m ≠ 0
Khi đó PT (2) có bốn nghiệm là: − t 2 ; − t 1 ; t 1 ; t 2
Bốn nghiệm này lập thành cấp số cộng khi :
− t 2 + t 1 = − 2 t 1 − t 1 + t 2 = 2 t 1 ⇔ t 2 = 3 t 1 ⇔ t 2 = 9 t 1
Theo định lý viet thì : t 1 + t 2 = 2 m + 1 t 1 t 2 = 2 m + 1
⇒ t 1 + 9 t 1 = 2 m + 1 t 1 9 t 1 = 2 m + 1 ⇔ 10 t 1 = 2 m + 1 ( * ) 9 t 1 2 = 2 m + 1 ( * * ) .
Từ (*) suy ra: 5 t 1 = m + 1 ⇔ m = 5 t 1 − 1 thay vào (**) ta được:
9 t 1 2 = 2 ( 5 t 1 − 1 ) + 1 ⇔ 9 t 1 2 − 10. t 1 + 1 = 0 ⇔ t 1 = 1 9 ⇒ m = − 4 9 t 1 = 1 ⇒ m = 4
Vậy m = 4 hoặc m = − 4 9 là những giá trị cần tìm
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 1 2021
1.
Do 3 nghiệm lập thành cấp số cộng \(\Rightarrow2x_2=x_1+x_3\)
Mà \(x_1+x_2+x_3=3m\)
\(\Rightarrow3x_2=3m\Rightarrow x_2=m\)
Thay lại pt ban đầu:
\(m^3-3m^3+2m\left(m-4\right)m+9m^2-m=0\)
\(\Leftrightarrow m^2-m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\)
- Với \(m=0\Rightarrow x^3=0\Rightarrow\) pt có đúng 1 nghiệm (ktm)
- Với \(m=1\Rightarrow x^3-3x^2-6x+8=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=1\\x=4\end{matrix}\right.\) (thỏa mãn)
Vậy \(m=1\)