Biết AC cắt BD tại O trung điểm mỗi đoạn.
Chứng minh:
a, AB//CD và AB=CD b, AD//BC và AD=BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2015
(hình hơi xấu =P)
a,Xét tam giác ABO và tam giác COD có:
BO=OD (vì O là TĐ của BD)
AO=OC (vì O là TĐ của AC)
AOB = DOC (đối đỉnh)
\(\Rightarrow\)tam giác ABO=tam giác COD (c.g.c)
\(\Rightarrow\)AB=CD (hai cạnh tương ứng)
và BAO=OCD (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong tạo bởi AC cắt AB và DC => AB song song với CD
b, Xét tam giác AOD và tam giác OCD có:
BO=OD (vì O là TĐ của BD)
AO=OC (vì O là TĐ của AC)
AOD=BOC (đối đỉnh)
\(\Rightarrow\)tam giác AOD=tam giác OCD (c.g.c)
\(\Rightarrow\)AD=BC (hai cạnh tương ứng)
và BCO=OAD (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong tạo bởi AC cắt BC và AD => BC song song với AD
*Lưu ý: những chữ số viết liền nhau mà không ghi chữ "tam giác'' (như ABC) xin tự hiểu là góc
DL
24 tháng 8 2016
bn ơi!
bn ko cho pyt đó là hình j thỳ sao nó cắt nhau đây?
lại 1 mâu thuẫn nữa: AB// BD(gt) z làm sao mà nó cắt nhau?
16 tháng 12 2016
mình ko biết cách c/m thẳng hàng ở câu c thôi ai giúp với
15 tháng 11 2023
a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{AOD}=\widehat{COB}\)
OD=OB
Do đó: ΔOAD=ΔOCB
=>AD=CB và \(\widehat{OAD}=\widehat{OCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
b: Xét ΔOAB và ΔOCD có
OA=OC
\(\widehat{AOB}=\widehat{COD}\)
OB=OD
Do đó: ΔOAB=ΔOCD
=>AB=CD
Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
Do đó: ΔABC=ΔCDA
=>\(\widehat{ABC}=\widehat{CDA}\)
c: Xét ΔOBN và ΔODM có
OB=OD
\(\widehat{OBN}=\widehat{ODM}\)
BN=DM
Do đó: ΔOBN=ΔODM
=>\(\widehat{BON}=\widehat{DOM}\)
mà \(\widehat{DOM}+\widehat{BOM}=180^0\)
nên \(\widehat{BON}+\widehat{BOM}=180^0\)
=>\(\widehat{MON}=90^0\)
=>M,O,N thẳng hàng
d: Xét ΔOAE và ΔOCF có
OA=OC
\(\widehat{AOE}=\widehat{COF}\)
AE=CF\(\left(AE=\dfrac{AD}{2}=\dfrac{BC}{2}=CF\right)\)
Do đó: ΔOAE=ΔOCF
=>\(\widehat{AOE}=\widehat{COF}\)
mà \(\widehat{AOE}+\widehat{EOC}=180^0\)
nên \(\widehat{COF}+\widehat{COE}=180^0\)
=>\(\widehat{FOE}=180^0\)
=>F,O,E thẳng hàng
mà OE=OF
nên O là trung điểm của EF
26 tháng 11 2023
1:
a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
AB=CD
\(\widehat{OBA}=\widehat{ODC}\)(hai góc so le trong, AB//CD)
Do đó: ΔOAB=ΔOCD
=>OA=OC và OB=OD
=>O là trung điểm chung của AC và BD
b: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{AOD}=\widehat{COB}\)
OD=OB
Do đó: ΔOAD=ΔOCB
=>\(\widehat{OAD}=\widehat{OCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
c: ΔOAD=ΔOCB
=>AD=BC
2:
a: Xét ΔAHO vuông tại H và ΔCKO vuông tại K có
OA=OC
\(\widehat{AOH}=\widehat{COK}\)
Do đó: ΔAHO=ΔCKO
=>AH=CK và OH=OK
b: Xét ΔAOK và ΔCOH có
OA=OC
\(\widehat{AOK}=\widehat{COH}\)
OK=OH
Do đó; ΔAOK=ΔCOH
=>\(\widehat{OAK}=\widehat{OCH}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AK//CH
c: OH=OK
H,O,K thẳng hàng
Do đó: O là trung điểm của HK
d: AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
=>AE//CF
Xét tứ giác AECF có
AE//CF
AF//CE
Do đó: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nen O là trung điểm của EF
3: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
4: Xét ΔOIB và ΔOVD có
\(\widehat{IBO}=\widehat{VDO}\)
OB=OD
\(\widehat{IOB}=\widehat{VOD}\)
Do đó: ΔOIB=ΔOVD
=>BI=DV
CM
24 tháng 5 2019
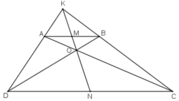
Gọi KO cắt AB, CD lần lượt tại M, N.
ΔKDN có AM // DN (A ∈ KD, M ∈ KN) ⇒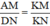 
(Hệ quả định lý Ta-let)
ΔKCN có BM // CN (M ∈ KN, B ∈ KC) ⇒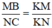 
(Hệ quả định lý Ta-let)
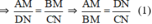
ΔOCN có AM // NC (A ∈ OC, M ∈ ON) ⇒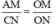 
(Hệ quả định lý Ta-let)
ΔODN có MB // ND (M ∈ ON, B ∈ OD) ⇒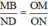 
(Hệ quả định lý Ta-let)
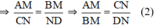
Từ (1) và (2) suy ra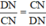 
⇒ CN = DN ⇒ AM = MB
Vậy M, N là trung điểm AB, CD.
Xét \(\Delta\)AOB và \(\Delta\)COD. TA CÓ:
BO=OD
OA=OC
AOB=COD(đối đỉnh)
=> \(\Delta\)AOB=\(\Delta\)COD(c-g-c)
=>AOB=COD(hai góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AB//CD