Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H. AO cắt BC tại M. P, Q lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Chứng minh:
a/ H là tâm đường tròn nội tiếp tam giác DEF
b/ HE.MQ= HF. MP
c/ \(\dfrac{MB}{MC}.\dfrac{DB}{DC}=\left(\dfrac{AB}{AC}\right)^2\)



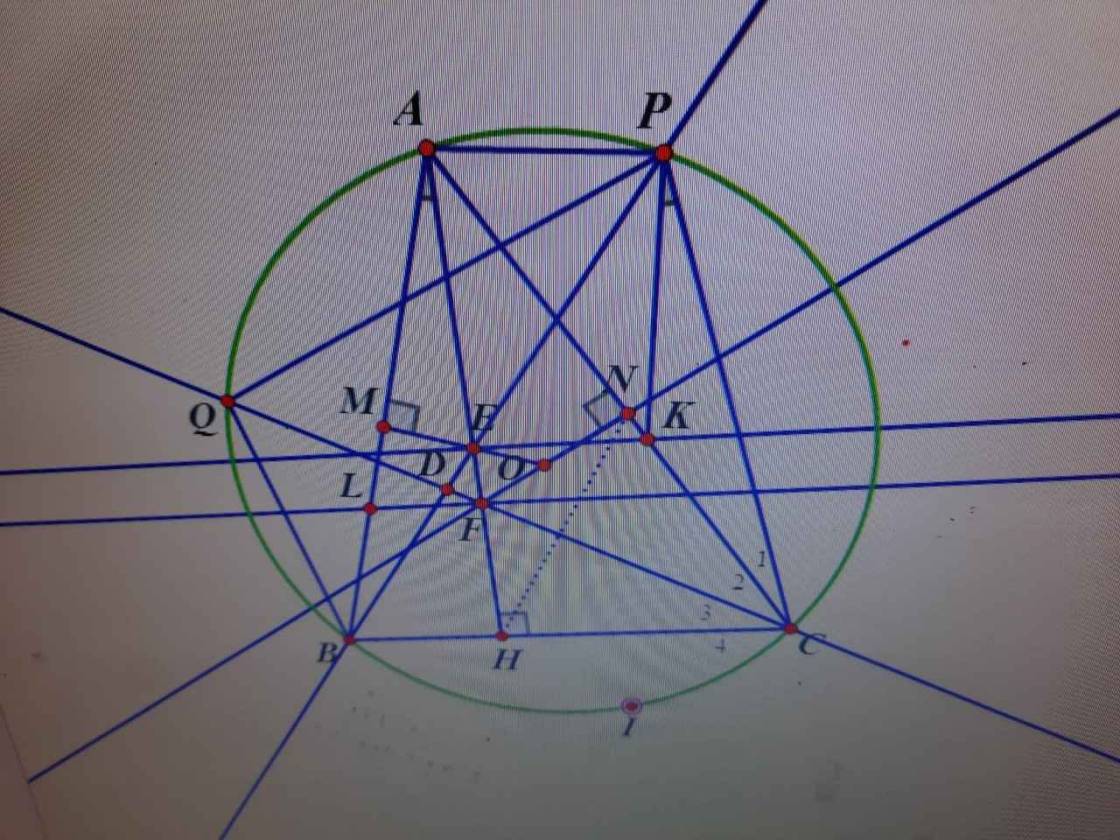
help meeee!