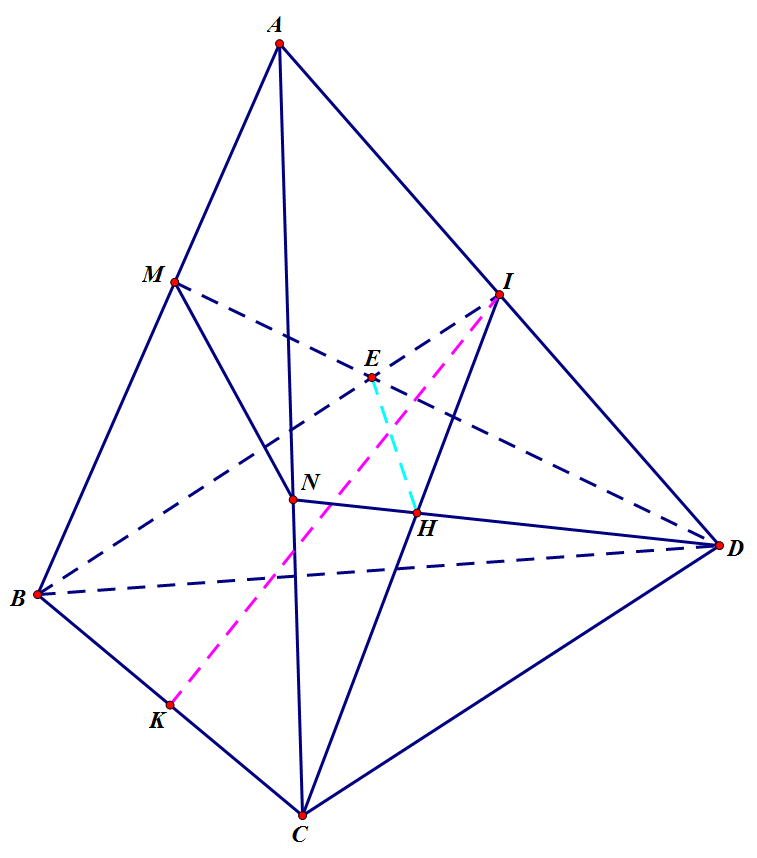
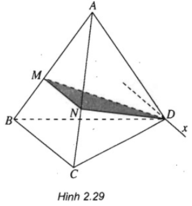
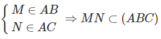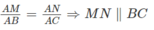Bài 5. Cho tứ diện ABCD.Trên cạnh AB lấy điểm M, trong tam giác BCD lấy điểm N. Tìm giao điểm:
a) BC và (DMN) b) AC và (DMN) c) MN và (ACD)
Vẽ hình
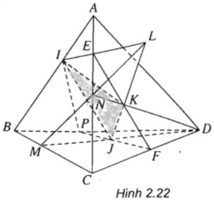
Bài 6. Cho tứ diện ABCD. Trên các cạnh AB,AC lấy 2 điểmM,N; trong tam giác BCD lấy điểm P.Tìm các giao điểm sau:
a) MP và (ACD) b) AD và (MNP) c) BD và (MNP)
Vẽ hình