Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
1: Xét ΔAOM và ΔBOM có
OA=OB
OM chung
AM=BM
Do đó: ΔOAM=ΔOBM
2: Xét ΔMNA và ΔMOB có
MN=MO
\(\widehat{NMA}=\widehat{OMB}\)(hai góc đối đỉnh)
MA=MB
Do đó: ΔMNA=ΔMOB
3: Ta có: ΔMNA=ΔMOB
=>NA=OB
Ta có: ΔMNA=ΔMOB
=>\(\widehat{MNA}=\widehat{MOB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//OB
Ta có: OB=AN
\(OK=KB=\dfrac{OB}{2}\)(K là trung điểm của OB)
\(AH=HN=\dfrac{AN}{2}\)(H là trung điểm của AN)
Do đó: OK=KB=AH=HN
Xét tứ giác OKNH có
OK//NH
OK=NH
Do đó: OKNH là hình bình hành
=>ON cắt KH tại trung điểm của mỗi đường
mà M là trung điểm của ON
nên M là trung điểm của KH
=>K,M,H thẳng hàng
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
b: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
a) Xét \(\Delta MDA\)và \(\Delta CDB\)có:
MD = DC (gt)
DA = DB (gt)
\(\widehat{MDA}=\widehat{BDC}\)(đối đỉnh)
=> \(\Delta MDA=\Delta CDB\left(c.g.c\right)\)
b) Vì \(\Delta MDA=\Delta CDB\left(cma\right)\Rightarrow\widehat{MAD}=\widehat{DBC}\)(2 góc tương ứng)
Mà \(\widehat{MAD}\)so le trong với \(\widehat{DBC}\)
=> AM // BC (đpcm)
c) Xét \(\Delta AEN\)và \(\Delta BEC\)có:
EN = BE (gt)
AE = EC (gt)
\(\widehat{AEN}=\widehat{BEC}\)(đối đỉnh)
\(\Rightarrow\Delta AEN=\Delta CEB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NAE}=\widehat{ECB}\)(2 góc tương ứng)
Mà \(\widehat{NAE}\)so le trong với \(\widehat{ECB}\)
\(\Rightarrow\)AN // BC
Ta có :
AN // BC
MA // BC
\(\Rightarrow AN\equiv MA\)
\(\Rightarrow\)M;A;N thẳng hàng (đpcm)
a: Xet ΔANO vuông tại N và ΔBNF vuông tại N có
NA=NB
NO=NF
=>ΔANO=ΔBNF
=>AO=BF và góc NAO=góc NBF
=>AO//BF
b: Xét tứ giác AECO có
P là trung điểm chung của AC và EO
=>AECO là hình bình hành
=>AO//CE và AO=CE; OC//AE và OC=AE
=>FB//CE và FB=CE
Xét tú giác BOCD có
M là trung điểm chung của BC và OD
=>BOCD là hình bình hành
=>BD//OC và BD=OC; OB//DC và OB=DC
=>AE//BD và AE=BD; AF//CD và AF=CD
AE=BD=CO
CD=AF=BO
BF=CE=AO
mà BO=AO=CO
nên AE=BD=CD=AF=BF=CE
=>ĐPCM
a: Xét ΔANO và ΔBNF có
NA=NB
góc ANO=góc BNF
NO=NF
=>ΔANO=ΔBNF
=>AO=BF và góc NAO=góc NBF
=>AO//BF
c: Xét ΔODE có OM/OD=OP/OE
nên MP//DE và MP=1/2DE
Xet ΔBAC có CM/CB=CP/CA=1/2
nên MP//AB và MP=1/2AB
=>DE=AB
Xét ΔODF có OM/OD=ON/OF=1/2
nên MN//FD và MN=1/2FD
Xét ΔBAC có BM/BC=BN/BA=1/2
nên MN//AC và MN=1/2AC
=>FD=AC
Xét ΔOEF có OP/OE=ON/OF=1/2
nên NP//FE và NP=1/2FE
Xét ΔABC có AN/AB=AP/AC
nên NP//BC và NP=1/2BC
=>FE=BC
=>ΔABC=ΔDEF
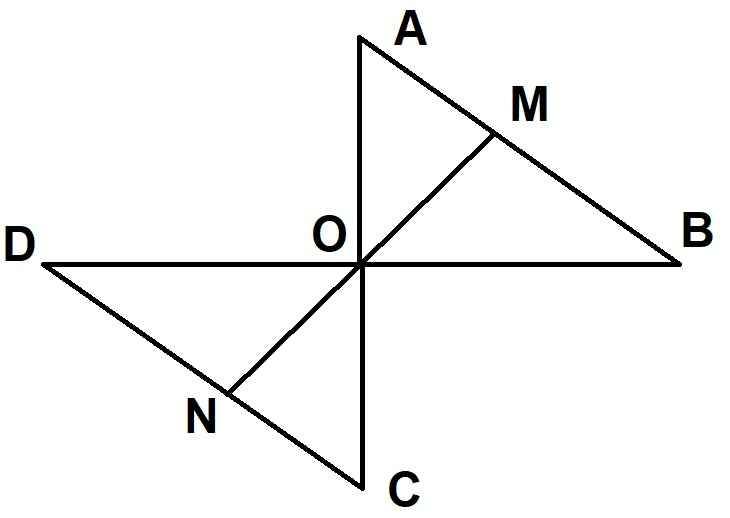
a) xét tứ giác BDCO có:
M là trung điểm BC (gt)
D là điểm đối xứng của O qua M (D thuộc tia đối MO; MO=MD)
=> tứ giác BDCO là hình bình hành (vì có 2 đường chéo cắt nhau tại giao điểm)
=> OB=DC và OB//CD (tính chất hình bình hành)
b) xét tam giác COM có: OM=MC (do OD và BC cắt nhau tại giao điểm)
=> tam giác COM là tam giác cân tại M
xét tam giác cân COM cân tại M có E là trung điểm của OC
=> ME là đường trung tuyến của tam giác cân COM
mà trong tam giác cân đường trung tuyến trùng với đường cao
=> ME là đường cao của tam giác COM => ME _|_ OC
Mà E là trung điểm OC => ME là đường trung trực của đường thẳng OC
xét tứ giác OMCK có: ME là đường trung trực của OC
=> tứ giác OMCK là hình thoi
=> CK//OM và OK//MC (tính chất hình thoi)
c) Ở trên câu b) chứng minh rồi