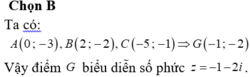Biểu diễn các điểm A(5;0); B(5;-3) trên mặt phẳng tọa độ và xác định điểm đối xứng vs A;B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


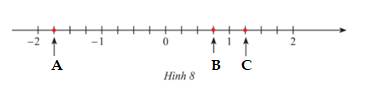
a) Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)
b) Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)
Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:


a) HS tự biểu diễn. b) Các số nguyên âm gồm có: -4; -3; -2. HS tự biểu diễn. c) Không

Từ bài ra ta có A(0;3),B(2;-2),C(-5;-1)
⇒ Trọng tâm G của tam giác ABC có tọa độ
x G = x A + x B + x C 3 = 0 + 2 + ( - 5 ) 3 = - 1 y G = y A + y B + y C 3 = - 3 + ( - 2 ) + ( - 1 ) 3 = - 2
⇒ G(-1;-2)
Điểm G(-1;-2) biểu diễn số phức z=-1-2i.
Chọn đáp án B.

a) Biểu diễn các số –3; –4; 2; 4 trên trục số.
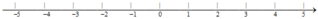
b) Ghi các số nguyên âm nằm giữa các số –5 và –1 trên trục số.
c) Trên trục số không có điểm nào biểu diễn số nguyên âm nằm giữa –5 và –4

Ta có: \(\frac{{25\pi }}{3} = \frac{\pi }{3} + 4.2\pi .\) Do đó điểm biểu diễn cung lượng giác \(\frac{{25\pi }}{3}\) trùng với điểm biểu diễn cung lượng giác \(\frac{\pi }{3}\).
Vậy ta chọn đáp án A