Một ô tô chuyển động trên các đoạn đường thẳng liên tiếp AB, BC, CD có chiều dài bằng nhau và bằng 36 km,
coi tốc độ chuyển động của ô tô trên mỗi đoạn đường là không đổi. Trên đoạn AB xe chuyển động với tốc độ
v 0 , trên đoạn BC tốc độ của xe bằng 0,8v 0 , trên đoạn CD tốc độ của xe là 0,75v 0 , thời gian xe chuyển động từ B
đến D là 1 giờ 15 phút. Tìm v 0 và tốc độ trung bình của xe trên cả quãng đường AD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là D
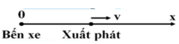
Ta có: x = x0 + vt
→ x 0 = + 8 ( km ) v = 60 ( km / h )
=> x = 8 + 60t (km; h).

Chọn A.
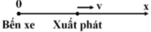
Đối chiếu với phương trình tổng quát: x = x 0 + v t ⇒ x 0 = + 5 ( k m ) v = 80 ( k m / h ) ⇒ x = 5 + 80 t

Vận tốc trung bình của ô tô trên cả đoạn đường là
\(v_{tb}=\dfrac{\left(v_1+v_2+v_3\right)}{3}=\dfrac{12+8+16}{3}=12\left(ms\right)\)
Đổi 12m/s = 43,2 kmh
Vận tốc trung bình của ô tô trên cả chặng đường là:
\(V_{tb}=\dfrac{2v_1.\left(v_2+v_3\right)}{2v_1+v_2+v_3}=\dfrac{2.12\left(8+16\right)}{2.12+8+16}=12\dfrac{m}{s}\)

Vận tốc trung bình của ô tô trên cả chặng đường là
\(v_{tb}=\dfrac{v_1+v_2+v_3}{3}=\dfrac{12+8+16}{3}=12\left(ms\right)\)

Vận tốc trung bình của xe là:\( v=\dfrac{s}{\dfrac{s}{2}(\dfrac{1}{v_1}+\dfrac{1}{v_2})} =\dfrac{1}{\dfrac{1}{2}(\dfrac{1}{ 50 }+\dfrac{1}{ 30 })} =37,5(km/h)\)


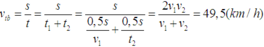

1 giờ 15 phút=1,25 giờ
Vận tốc xe đi đoạn BD là: \(v=\frac{s}{t}=\frac{BC+CD}{1,25}=\frac{72}{1,25}=57,6̸\) (km/h)
Ta có: \(0,8v_o+0,75v_o=57,6\)
\(\Rightarrow v_o.\left(0,8+0,75\right)=57,6\)
\(\Rightarrow v_o=\frac{1152}{31}\) (km/h)
Thời gian xe đi hết AB:\(t_1=\frac{s}{v_o}=\frac{36}{\frac{1152}{31}}=\frac{31}{32}\left(h\right)\)
Thời gian xe đi hết BC:\(t_2=\frac{s}{0,8v_o}=\frac{36}{0,8.\frac{1152}{31}}=\frac{155}{128}\left(h\right)\)
Thời gian xe đi hết CD:\(t_3=\frac{s}{0,75v_o}=\frac{36}{0,75.\frac{1152}{31}}=\frac{31}{24}\left(h\right)\)
\(\Rightarrow v_{TB}=\frac{3s}{t_1+t_2+t_3}=\frac{3.36}{\frac{31}{32}+\frac{155}{128}+\frac{31}{24}}\simeq31\)(km/h)