Với a ≥ 0, b ≥ 0, chứng tỏ √(a2 b) =...
Đọc tiếp
Với a ≥ 0, b ≥ 0, chứng tỏ √(a2 b) = a√b.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 5 2018
√ ( a 2 b ) = √ ( a 2 ) . √ b = | a | √ b = a √ b ( d o a ≥ 0 ; b ≥ 0 )
M
3
3 tháng 8 2021
\(\sqrt{a^2b}=\left|a\right|\sqrt{b}=a\sqrt{b}\)( vì a >= 0 )
PT
1
CM
28 tháng 10 2018
Từ (1) và (2) suy ra: a 2 < b 2
Ta có: a < b ⇒ a 3 < a 2 b (3)
a < b ⇒ a b 2 < b 3 (4)
a < b ⇒ a.a.b < a.b.b ⇒ a 2 b < a b 2 (5)
Từ (3), (4) và (5) ⇒ a 3 < b 3
PT
1
CM
19 tháng 12 2019
Với a > 0, b > 0 ta có:
a < b ⇒ a.a < a.b ⇒ a 2 < ab (1)
a < b ⇒ a.b < b.b ⇒ ab < b 2 (2)
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 5 2019
a/
Do \(\left\{{}\begin{matrix}a>2\Rightarrow\frac{1}{a}< \frac{1}{2}\\b>2\Rightarrow\frac{1}{b}< \frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\frac{1}{a}+\frac{1}{b}< \frac{1}{2}+\frac{1}{2}=1\)
\(\Rightarrow\frac{a+b}{ab}< 1\Rightarrow a+b< ab\) (đpcm)
b/ Ko rõ đề là gì
c/ \(\frac{a^2+b^2}{2}\ge ab\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\Leftrightarrow\left(a-b\right)^2\ge0\) (luôn đúng)
Vậy BĐT được chứng minh
CM
24 tháng 1 2019
a) Biến đổi vế trái:
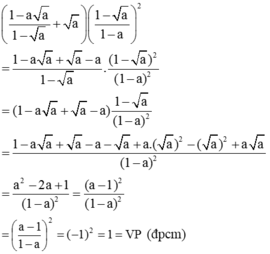
b) Biến đổi vế trái:
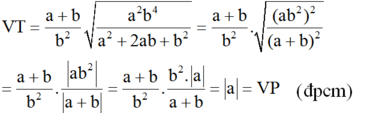
( v ì a + b > 0 n ê n | a + b | = a + b ; b 2 > 0 )
Ta có \(\sqrt{a^2b}\)
\(=\sqrt{a^2}.\sqrt{b}\)
\(=\left|a\right|\sqrt{b}\)
\(=a\sqrt{b}\)(vì a \(\ge0;b\ge0\))
Tham khảo :
√(a2 b) = √(a2 ).√b = | a | √b = a√b (do a ≥ 0;b ≥ 0)
Cre : https://khoahoc.vietjack.com/