Giúp em giải câu này với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x-2+2}{x-2}+\dfrac{1}{y+1}=3\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{1}{y+1}=2\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{x-2}+\dfrac{3}{y+1}=6\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x-2}=7\\\dfrac{2}{x-2}+\dfrac{1}{y+1}=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-2=\dfrac{10}{7}\\\dfrac{1}{y+1}=\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{24}{7}\\y=\dfrac{2}{3}\end{matrix}\right.\)

Vì \(\sqrt{3\sqrt{2\sqrt{x}}}\) là số nguyên => \(3\sqrt{2\sqrt{x}}\) là số chính phương.
Mà 3 là số nguyên tố nên \(\sqrt{2\sqrt{x}}\)có dạng \(3k^2\) với k ∈ N*
\(\sqrt{2\sqrt{x}}=3k^2\Leftrightarrow2\sqrt{x}=9k^4\Leftrightarrow4x=81k^8\)\(\Leftrightarrow x=\dfrac{81}{4}k^8\)
Vì x là số có 4 chữ số => \(x\le9999\) => \(\dfrac{81}{4}k^8\le9999\Leftrightarrow k^8\le\dfrac{4444}{9}\Leftrightarrow k^8\le493\) (1)
Vì \(k\ge1\) => \(k^8\ge1\) (2)
Từ (1) và (2), ta có \(k^8\in\left\{1,256\right\}\)
-Xét \(k^8=1\Rightarrow k=1\Rightarrow x=\)\(\dfrac{81}{4}\) => Vô lí
-Xét \(k^8=256\Rightarrow k=2\Rightarrow x=5184\) t/m
Vậy x = 5184

\(\left(2x+1\right)^2=81\)
\(\Rightarrow\left[{}\begin{matrix}2x+1=9\\2x+1=-9\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=8\\2x=-10\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-5\end{matrix}\right.\)


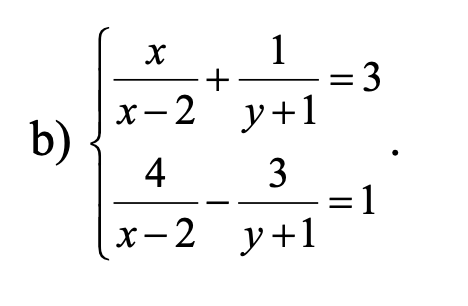

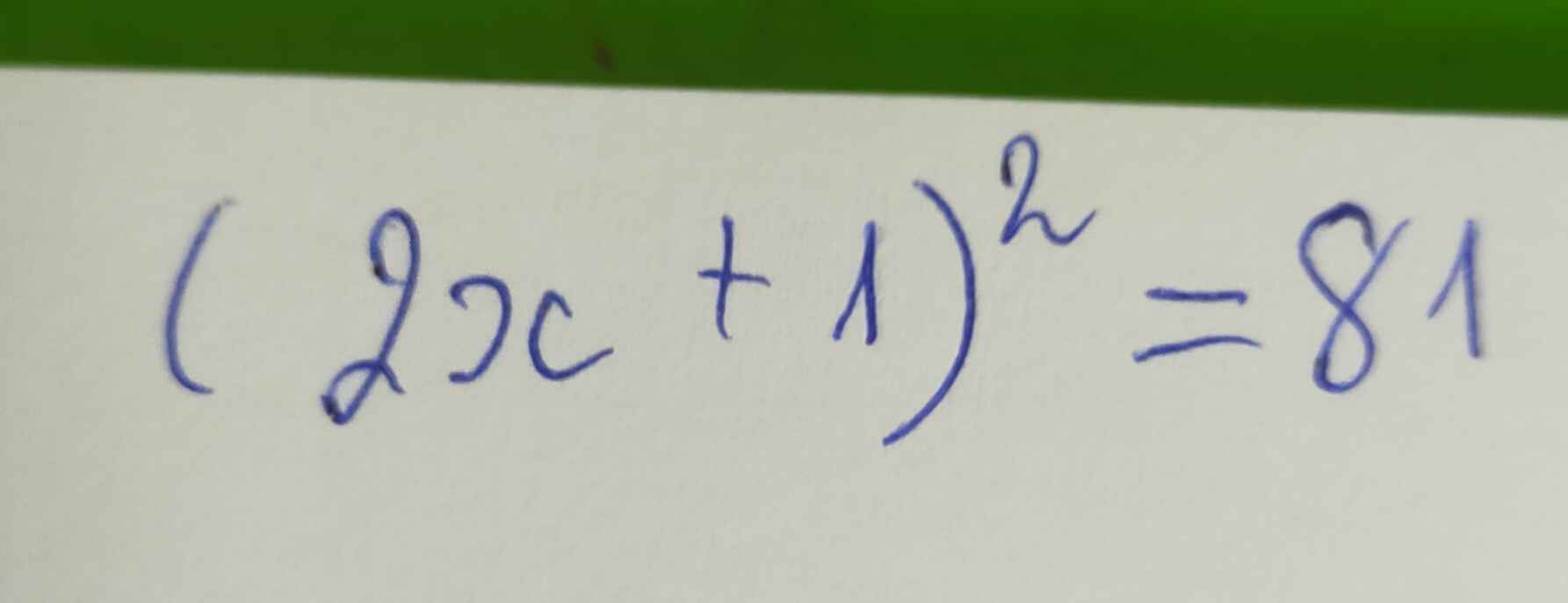
Chọn C.
Số cần lập là \(\overline{abcd}\)
Chọn a\(\ne\)0 có 4 cách chọn.
Chọn b\(\ne a\) có 4 cách chọn.
Chọn c\(\ne\) a,b có 3 cách chọn.
Chọn d\(\ne\) a,b,c có 2 cách chọn.
\(\Rightarrow\) Có tất cả \(4\cdot4\cdot3\cdot2=96\) số được lập.