Biết rằng khi m = m\(_0\) thì hàm số \(y=\)\(-x^2+2x+m-4\) đạt giá trị lớn nhất trên đoạn \([-1;2]\) bằng 3. Mệnh đề nào sau đây đúng?
A. m\(_0\) \(\in\) \((-\infty;5)\)
B. m\(_0\) \(\in\) \([7;8)\)
C. m\(_0\) \(\in\) \((5;7)\)
D. m\(_0\) \(\in\)...
Đọc tiếp
Biết rằng khi m = m\(_0\) thì hàm số \(y=\)\(-x^2+2x+m-4\) đạt giá trị lớn nhất trên đoạn \([-1;2]\) bằng 3. Mệnh đề nào sau đây đúng?
A. m\(_0\) \(\in\) \((-\infty;5)\)
B. m\(_0\) \(\in\) \([7;8)\)
C. m\(_0\) \(\in\) \((5;7)\)
D. m\(_0\) \(\in\) \((9;11)\)
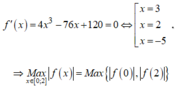
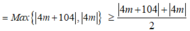
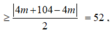
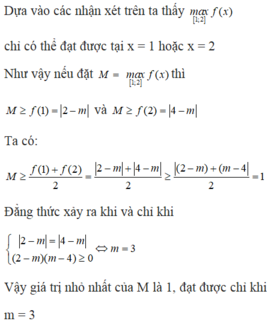
\(a=-1< 0;\) \(-\frac{b}{2a}=1\in\left[-1;2\right]\)
\(\Rightarrow\) Hàm số đạt GTLN tại \(\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
\(y\left(-1\right)=m-7\) ; \(y\left(2\right)=m-12\)
Do \(m-7>m-12\) \(\forall m\)
\(\Rightarrow\max\limits_{\left[-1;2\right]}y=y\left(-1\right)\Rightarrow m-7=3\Rightarrow m=10\)
Đáp án D
cảm ơn rất nhiều ạ