Tìm số đo góc B, D trong hình sau:(hơi xấu)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


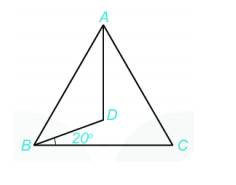
a, Các góc có trong hình vẽ là : \(\widehat{ABC} ; \widehat{BAC} ; \widehat{CAB} ; \widehat{BDA} ; \widehat{DAB} ; \widehat{ABD} ; \widehat{DBC} ; \widehat{DAC}\)
Những góc có số đo bằng 60 độ là : \(\widehat{ABC} ; \widehat{BAC} ; \widehat{CAB}\)
b, Điểm D có nằm trong góc ABC. Điểm C không nằm trong góc ADB.
c, Số đo góc ABD là: 40o.

a) Các góc kề với \(\widehat {tOz}\)là: \(\widehat {zOy},\widehat {zOn},\widehat {zOm}\)
b) Ta có: \(\widehat {mOn}\) = 30\(^\circ \) nên góc kề bù với \(\widehat {mOn}\) có số đo là: 180\(^\circ \) - 30\(^\circ \) = 150\(^\circ \)
c) Ta có:
\(\begin{array}{l}\widehat {mOn} + \widehat {nOy} + \widehat {yOt} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {nOy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {nOy} = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy \(\widehat {nOy} = 60^\circ \)
d) Ta có: \(\widehat {tOz} = 45^\circ \) nên góc kề bù với \(\widehat {tOz}\) có số đo là: 180\(^\circ \) - 45\(^\circ \) = 135\(^\circ \)

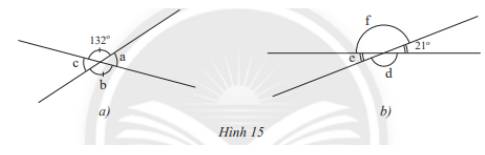
a) Ta có: b = 132\(^\circ \)( 2 góc đối đỉnh)
a + 132\(^\circ \) =180\(^\circ \) (2 góc kề bù) nên a = 180\(^\circ \) - 132\(^\circ \) = 48\(^\circ \)
c = a = 48\(^\circ \)(2 góc đối đỉnh)
b) e = 21\(^\circ \)(2 góc đối đỉnh)
d + 21\(^\circ \) =180\(^\circ \) (2 góc kề bù) nên d = 180\(^\circ \)- 21\(^\circ \)= 159\(^\circ \)
f = d =159\(^\circ \)(2 góc đối đỉnh)

a) Tìm các cặp góc so le trong: P2 và Q3; P3 và Q2
b) Tìm các cặp góc trong cùng phía: P2 và Q2; P3 và Q3
c) Tìm các cặp góc đồng vị: P1 và Q2; p2 và Q1; P3 và Q4' p4 và Q3
d) Tính số đo góc P4:
Ta có: Q2 = P1 = 50o ( 2 góc đồng vị)
Mà P4 + P1 = 180o ( 2 góc kề bù)
P4 = 180o - P1
P4 = 180o - 50o = 130o
Ta có: \(\widehat{B}+\widehat{D}+\widehat{C}+\widehat{A}=360^0\)
\(\Rightarrow\widehat{B}+\widehat{D}=360^0-90^0-150^0=120^0\)
\(\Rightarrow3x=120^0\Rightarrow x=40^0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{B}=2x-2.40^0=80^0\\\widehat{D}=x=40^0\end{matrix}\right.\)
c.ơn