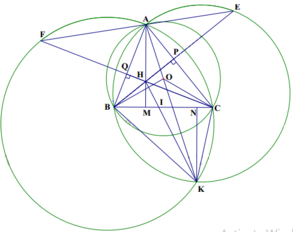
Cho ∆ABC. (K) đi qua BC sao cho (K) cắt đoạn CA và AB tại E,F. BE cắt CF tại H. Gọi M là trung điểm của EF. Gọi P,Q lần lượt là đối xứng của A qua BE,CF
Chứng minh rằng (I) ngoại tiếp ∆HEP và (J) ngoại tiếp∆HFQ cắt nhau trên AM.
Chứng minh (I) và (J) có bán kính bằng nhau.