Cho tam giác ABC vuông tại A AB lớn hơn AC M là trung điểm của BC trên tia đối của ma lấy điểm D sao cho MD = ma a Chứng minh AB = BC và AB song song bc B Chứng minh tam giác ABC bằng tam giác bda Từ đó suy ra AM = BC chia 2 trên tia đối của AC lấy điểm E sao cho ae = AC Chứng minh Be song song AM đề tìm điều kiện của tam giác ABC để AC = BC chia 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 4 2021
a) Sửa đề: ΔAMB=ΔDMC
Xét ΔAMB và ΔDMC có
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔDMC(c-g-c)
GN
22 tháng 4 2018
a, áp dụng tổng 3 góc trong 1 tam giác => góc AB= 25 độ
AC < AB ( 65 độ > 25 độ)
b, Xét tam giác BHC và tam giác BHE có: BH- chung ; BHA = BHE (=90 độ) ; AH = HE ( theo đề bài)
=> hai tam giác bằng nhau (c.g.c) => BA = BE => tam giác BEA cân tại B (đpcm)
c, Dễ dàng chứng minh được tam giác BEC = tam giác BAC
=> BEC = BAC = 90 độ
=> tam giác BEC vuông tại E (đpcm)
d, Ta có: MH đi qua trung điểm của AD và AE trong tam giác ADE => NM là đường trung bình của tam giác này => MN // DE (đpcm)
Youcho tam giác nhọn ABC, AB<AC. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD a) chứng minh tam giác AMB=tam giác DMC b) chứng minh AB=DC c)chứng minh AB song song với CD
H9
HT.Phong (9A5)
CTVHS
16 tháng 1
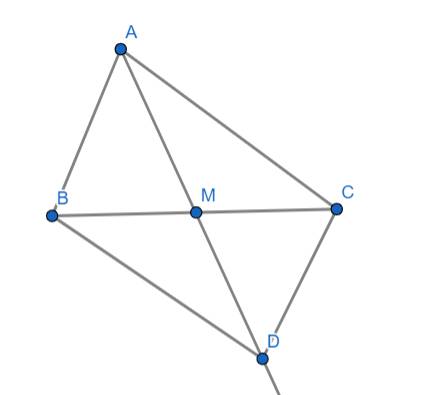
a) Xét ΔAMB và ΔDMC có:
\(AM=CM\) (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(BM=CM\) (M là trung điểm của BC)
\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)
b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow AB=DC\) (2 cạnh t.ứng)
c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
15 tháng 7 2016
Xét tam giác ABM và tam giác DCM có:
AM=MD
góc AMB=góc CMD ( đối đỉnh)
BM=CM ( M là trung điểm của BC)
=> tam giác ABM=tam giác DCM( c.g.c)
b) theo a): tam giác ABM=tam giác DCM => góc BAM=góc D
mà chúng là hai góc so le trong => AB//DC
c) Vì AB=AC=> tam giác ABC cân tại A
tam giác ABC có AM là đường trung tuyến nên đồng thời là đường trung trực => AM vuông góc vs BC
d) Để góc ADC=30 độ thì góc BAM=30 độ
=> góc B= 90 độ-30 độ=60 độ
tam giác ABC cân tai A có góc B =60 độ
=> tam giác ABC đều
Vậy tam giác ABC đều thì góc ADC=30 độ
16 tháng 12 2018
a/ - AB = AC ( gt )
ABM = ACM vì { - AM chung
(c.c.c) - MB = MC ( m là trung điểm )
b/ AB // DC k phải AB // BC
T/g ABM = t/g DCM ( c.g.c)
AM = DM ( gt )
Góc AMB = DMC ( đđ )
BM = CM ( gt )
Có ABM = DCM ( t/g ABM = t/g DCM )
Lại ở vị trí slt
=> AB // DC
c/
AB = AC ( gt )
=> ABC cân tại A
Có AM là trung tuyến ( m là trug điểm )
=> AM là đường cao ABC
=> AM vuông góc BC
Hình như đề sai???