GIẢI GIÚP MÌNH BÀI NÀY VỚI MÌNH ĐANG CẦN GẤP!!!!!!!!!!!
Cho tứ giác ABCD có góc ABC=góc ADC và góc ABC+góc BCD<180 độ . Gọi E là giao điểm của 2 đường thẳng AB,CD . Chứng minh rằng : \(AC^2=CD.CE-AB.AE\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 7 2019
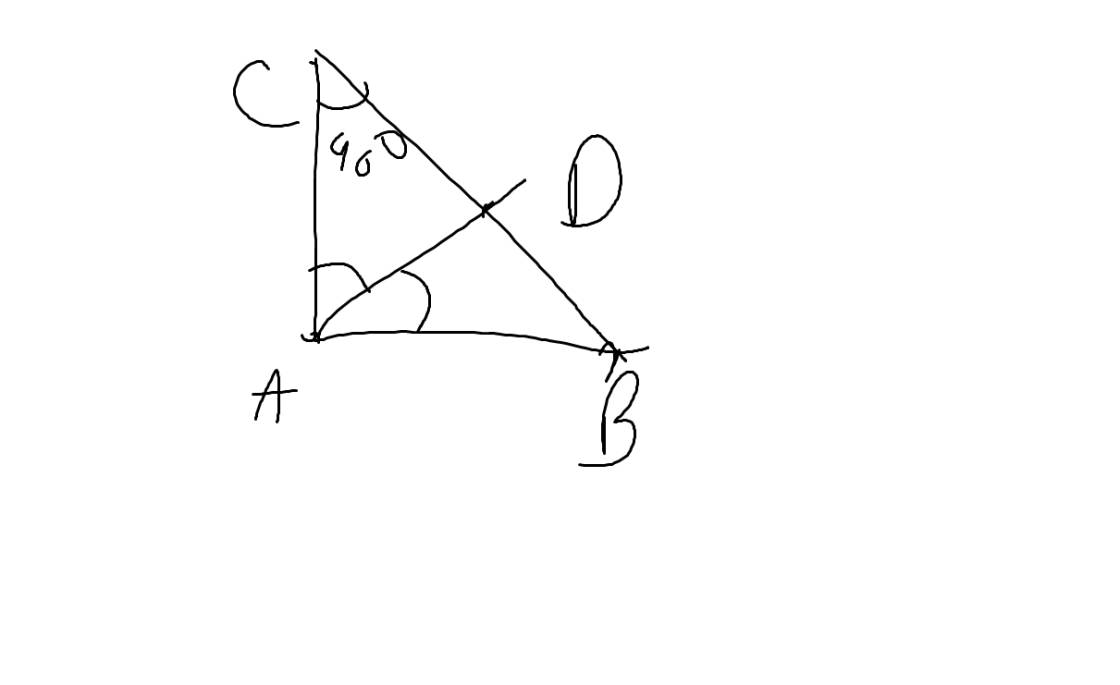
Vì BD là phân giác của ABC và ADC
Xét ∆ADB ta có :
A + ABD + ADB = 180°
ABD + ADB = 180 - 85 = 95°
Mà 2ABD + 2ADB = 95°
=> ABC + ADC = 95 * 2 = 190°
Mà A + ABC + ADC + C = 360°
=> C = 360 - 85 - 190 = 85°
19 tháng 8 2021
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=9\cdot25=225\\AC^2=16\cdot25=400\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{15}{25}=\dfrac{3}{5}\)
\(\Leftrightarrow\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 9 2021
1.
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)
23 tháng 11 2023
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+40^0=90^0\)
=>\(\widehat{ABC}=50^0\)
AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{BAC}}{2}=\dfrac{90^0}{2}=45^0\)
Xét ΔADB có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{DAB}+\widehat{ABD}=45^0+50^0=95^0\)
\(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
=>\(\widehat{ADB}+95^0=180^0\)
=>\(\widehat{ADB}=85^0\)
R
6 tháng 11 2015
tick cho mình đi rồi mình gửi bài cho còn không tick thì mình không bày đâu nhé
Từ giao điểm 3 đường trung trực tgiac EAD vẽ đ/tròn tâm giao điểm đó, cắt AC tại I
Tứ giác IEDA nội tiếp nên CA.CI=CD.CD.CE
Mặt khác góc EIA=ADC=ABD nên tứ giác IECB nội tiếp nên ta có
CA.AI=AB.AE(1)
Trừ 1 cho 2 đc ĐPCM
Trên tia đối CA lấy điểm I sao cho góc AIE=ADC
Xét \(\Delta ADC\&\Delta EIC\) có
\(\widehat{ADC}=\widehat{AIE}\)
chung \(\widehat{ACD}\)
\(\Rightarrow\Delta ADC\sim\Delta EIC\left(g-g\right)\Rightarrow\frac{AC}{EC}=\frac{DC}{IC}\Rightarrow AC.CI=EC.DC\left(1\right)\)
Xét \(\Delta BAC\&\Delta EAI\) có
\(\widehat{ABC}=\widehat{AIE}\left(=\widehat{ADC}\right)\)
\(\widehat{BAC}=\widehat{IAE}\left(dd\right)\)
Suy ra \(\Delta BAC\sim\Delta IAE\left(g-g\right)\Rightarrow\frac{AB}{AI}=\frac{AC}{AE}\Rightarrow AC.AI=AB.AE\left(2\right)\)
Cộng (1) và (2) có \(AC\left(AI+IC\right)=AB.AE+CD.CE\Rightarrow AC^2=...\)