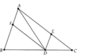
Cho tam giác ABC, AM là đường trung tuyến, AD là đường phân giác. Đường thẳng qua M và song song với AD cắt AB tại E và AC tại F. Chứng minh:
a) Tam giác AEF cân
b) AC-AB=2AE
P/s : Giúp mik với ạ . Thankiuuu :33
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .

1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.

Chứng minh tứ giác AEDF là hình thoi
Þ EF là phân giác của A E D ^
Theo câu b thì e thiếu đề : Cho Tam giác ABC với AC > AB
a) Ta có:
AD là phân giác ^BAC của \(\Delta\)ABC => ^BAD = ^CAD (1)
FM // AM => ^CFM = ^CAD ( đồng vị ) mà ^CFM = ^AFE ( đối đỉnh ) => ^CAD = ^AFE ( 2)
AD//EM => ^BAD = ^BEM (3)
Từ (1) ; (2) ; (3) => ^BEM = ^AFE => ^AEF = ^AFE => \(\Delta\)AEF cân tại A
b) Trên AC lấy điểm N sao cho AN = AB
=> \(\Delta\)ANB cân tại A
Gọi H là giao điểm của AD và và BN => AH là đường phân giác ^BAN
mà \(\Delta\)ANB cân tại A
=> AH là đường trung tuyến của \(\Delta\)ANB => H là trung điểm BN
Mặt khác có: M là trung điểm BC
=> HM là đường trung bình của \(\Delta\)NBC => HM // = \(\frac{1}{2}\)NC (4)
=> HM // AF
Ta lại có: AH //FM ( vì AD // FM )
=> AFMH là hình bình hành => AF = HM mà AE = AF ( vì \(\Delta\)AEF cân tại A )
=> AE = HM (5)
Từ (4) ; (5) => NC = 2 AE
=> AC - AB = AC - AN = NC = 2AE
Vậy AC - AB = 2AE.
Dạ em cảm ơn nhìu ạ :33