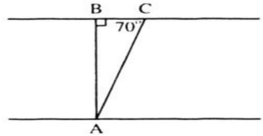
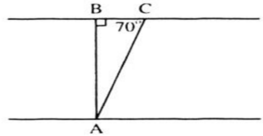
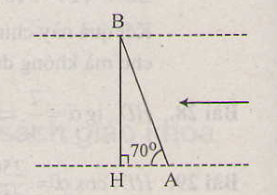
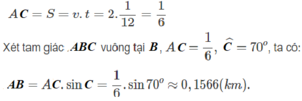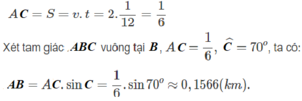Bài 3. Một con thuyền vượt qua một khúc sông nước chảy mạnh. Biết rằng đường đi của thuyền tạo với bờ một góc ![]() . Biết chiều rộng của khúc sông đó là 300m.
. Biết chiều rộng của khúc sông đó là 300m.
a) Tính quãng đường mà con thuyền đã đi.
b) Tính thời gian của con thuyền khi vượt qua khúc sông đó biết vận tốc của nó là 20m/phút ( kết quả làm tròn đến mét, phút) KO