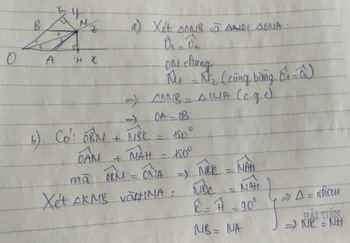Cho 3 tia ox, oy, oz cắt 2 đường thẳng song song m, m' lần lượt tại A, A' ∈ ox B, B'∈ oy ; C, C' ∈ oz. Chứng minh rằng \(\frac{AB}{A'B'}=\frac{BC}{B'C'}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A .
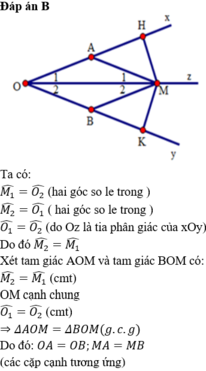
Vì OA // MB ( giả thuyết )
=> Góc AOM = Góc OMB ( 1 )
Vì AM = OB ( giả thuyết )
=> Góc AMO = Góc MOB ( 2 )
Từ ( 1 ) và ( 2 )
=> Góc AOM = Góc MOB ; Góc AMO = Góc BMO
Vậy hình tam giác AMO = Hình tam giác BMO ( góc - cạnh - góc )
= > AO = OB ; MA = MB ( 2 cạnh tương ứng )

x O y A z B M H K
Giải:
a) Xét \(\Delta MOA,\Delta MOB\) có:
\(\widehat{AOM}=\widehat{OMB}\) ( cặp góc so le trong và AM // Oy )
OM: cạnh chung
\(\widehat{AMO}=\widehat{BOM}\) ( cặp góc so le trong và AM // Oy )
\(\Rightarrow\Delta MOA=\Delta MOB\left(g-c-g\right)\)
\(\Rightarrow OA=OB\) ( cạnh t/ứng )
\(\Rightarrow MA=MB\) ( cạnh t/ứng )
b) Xét \(\Delta HOM\) có: \(\widehat{HOM}+\widehat{HMO}=90^o\) ( do \(\widehat{H}=90^o\) )
Xét \(\Delta KOM\) có: \(\widehat{MOK}+\widehat{OMK}=90^o\) ( do \(\widehat{K}=90^o\) )
Mà \(\widehat{HOM}=\widehat{MOK}\left(=\frac{1}{2}\widehat{O}\right)\)
\(\Rightarrow\widehat{HMO}=\widehat{OMK}\)
Xét \(\Delta HOM,\Delta KOM\) có:
\(\widehat{HOM}=\widehat{KOM}\left(=\frac{1}{2}\widehat{O}\right)\)
OM: cạnh chung
\(\widehat{HMO}=\widehat{OMK}\) ( cmt )
\(\Rightarrow\Delta HOM=\Delta KOM\left(g-c-g\right)\)
\(\Rightarrow MH=MK\) ( cạnh t/ứng )
Vậy...