Giúp mình câu b, c với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

a: Khi x=3 thì \(A=\dfrac{3\cdot3}{3-2}=9\)
b: C=A+B
\(=\dfrac{3x}{x-2}-\dfrac{6}{x-2}-\dfrac{x^2+4x+4}{x^2-4}\)
\(=\dfrac{3x-6}{x-2}-\dfrac{x+2}{x-2}\)
\(=\dfrac{3x-6-x-2}{x-2}=\dfrac{2x-8}{x-2}\)
c: Để C nguyên thì 2x-4-4 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6\right\}\)

b: \(sin^2b+cos^2b=1\)
=>\(sin^2b=1-\dfrac{1}{5}=\dfrac{4}{5}\)
=>\(sinb=\dfrac{2}{\sqrt{5}}\) hoặc \(sinb=-\dfrac{2}{\sqrt{5}}\)
TH1: \(sinb=\dfrac{2}{\sqrt{5}}\)
\(tanb=\dfrac{2}{\sqrt{5}}:\dfrac{1}{\sqrt{5}}=2\)
cot b=1/tanb=1/2
TH2: \(sinb=-\dfrac{2}{\sqrt{5}}\)
\(tanb=\dfrac{-2}{\sqrt{5}}:\dfrac{1}{\sqrt{5}}=-2\)
cot b=1/tan b=-1/2
c: \(1+cot^2y=\dfrac{1}{sin^2y}\)
=>\(\dfrac{1}{sin^2y}=1+2=3\)
=>\(sin^2y=\dfrac{1}{3}\)
=>\(siny=\dfrac{1}{\sqrt{3}}\) hoặc \(siny=-\dfrac{1}{\sqrt{3}}\)
TH1: \(siny=\dfrac{1}{\sqrt{3}}\)
\(coty=\dfrac{cosy}{siny}\)
=>\(cosy=\dfrac{1}{\sqrt{3}}\cdot\left(-\sqrt{2}\right)=\dfrac{-\sqrt{2}}{\sqrt{3}}\)
\(tany=\dfrac{1}{coty}=\dfrac{-1}{\sqrt{2}}\)
TH2: \(siny=-\dfrac{1}{\sqrt{3}}\)
\(cosy=coty\cdot siny=\left(-\sqrt{2}\right)\cdot\dfrac{-1}{\sqrt{3}}=\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}\)
$tany=\frac{1}{coty}=\frac{-1}{\sqrt{2}}$

1: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25\)
=>\(BC=\sqrt{25}=5\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\BH\cdot BC=AB^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH\cdot5=3\cdot4=12\\BH\cdot5=3^2=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=\dfrac{12}{5}=2,4\left(cm\right)\\BH=\dfrac{9}{5}=1,8\left(cm\right)\end{matrix}\right.\)
2: Xét (B;3cm)
BA là bán kính
AC\(\perp\)BA tại A
Do đó: AC là tiếp tuyến của (B;3cm)




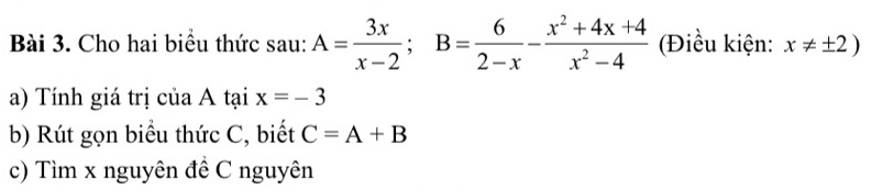

 giúp mình câu b) c) với ạ
giúp mình câu b) c) với ạ




 giải giúp mình câu b, c với ạ!
giải giúp mình câu b, c với ạ!

