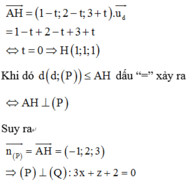Trong mặt phẳng xOy lập phương trình đường thẳng d cách A(1;1) một khoảng bằng 2 và cách B(2;3) một khoảng bằng 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 3 2022
d cách đều MN khi nó thỏa mãn 1 trong 2 trường hợp: d song song MN hoặc d đi qua trung điểm MN
TH1: d song song MN
\(\overrightarrow{MN}=\left(3;-4\right)\Rightarrow d\) nhận (4;3) là 1 vtpt
Phương trình d:
\(4\left(x+2\right)+3\left(y-3\right)=0\Leftrightarrow4x+3y-1=0\)
TH2: d đi qua trung điểm MN
Gọi P là trung điểm MN \(\Rightarrow P\left(\dfrac{1}{2};-1\right)\Rightarrow\overrightarrow{AP}=\left(\dfrac{5}{2};-4\right)=\dfrac{1}{2}\left(5;-8\right)\)
\(\Rightarrow d\) nhận (8;5) là 1 vtpt
Phương trình d:
\(8\left(x+2\right)+5\left(y-3\right)=0\Leftrightarrow8x+5y+1=0\)
Có 2 đường thẳng d thỏa mãn: \(\left[{}\begin{matrix}4x+3y-1=0\\8x+5y+1=0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Gọi \(\overrightarrow{n}=\left(a;b\right)\) là 1 vtpt của đường thẳng d' cần tìm
Do d' tạo với d 1 góc bằng 45 độ
\(\Rightarrow cos\left(d;d'\right)=\dfrac{\left|2a+3b\right|}{\sqrt{2^2+3^2}.\sqrt{a^2+b^2}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}\left|2a+3b\right|=\sqrt{13\left(a^2+b^2\right)}\)
\(\Leftrightarrow2\left(2a+3b\right)^2=13\left(a^2+b^2\right)\)
\(\Leftrightarrow5a^2-5b^2-24ab=0\)
\(\Rightarrow\left[{}\begin{matrix}a=5b\\b=-5a\end{matrix}\right.\) \(\Rightarrow\) chọn \(\left[{}\begin{matrix}\left(a;b\right)=\left(5;1\right)\\\left(a;b\right)=\left(1;-5\right)\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}5\left(x-3\right)+1\left(y-6\right)=0\\1\left(x-3\right)-5\left(y-6\right)=0\end{matrix}\right.\) \(\Leftrightarrow...\)
CM
23 tháng 8 2019
Đáp án A
Ta có: 
AM → (3; 2; 4)
Mặt phẳng (P) có vecto pháp tuyến là n p → (1; 1; 1)
Gọi H là hình chiếu vuông góc của A trên d. Ta có: d(A; d) = AH ≤ AM = 29
Dấu bằng xảy ra khi và chỉ khi H trùng M, nghĩa là d vuông góc với AM.
10 tháng 3 2022
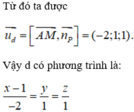
Gọi đường thẳng đi qua A là d'.
a) Ta có: \(d'\perp d.\)
\(\Rightarrow\) VTPT của d là VTCP của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\overrightarrow{u_{d'}}=\left(3;-4\right).\Rightarrow\overrightarrow{n_{d'}}=\left(4;3\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(4\left(x-2\right)+3\left(y+1\right)=0.\\ \Leftrightarrow4x+3y-5=0.\)
b) Ta có: \(d'//d.\)
\(\Rightarrow\) VTPT của d là VTPT của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\) \(\overrightarrow{n_{d'}}=\left(3;-4\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(3\left(x-2\right)-4\left(y+1\right)=0.\\ \Leftrightarrow3x-4y-10=0.\)
CM
21 tháng 12 2019
Đáp án D
Gọi H là hình chiếu của A trên đường thẳng d.
Ta có: AH ≤ AM nên khoảng cách từ A đến đường thẳng d nhỏ nhất khi AH trùng với mới AM, khi đó H trùng với M và AM vuông góc d. Mặt phẳng (P) có vecto pháp tuyến n p → (1; 1; 1) . AM → (0; -2; -1) Đường thẳng d nhận vecto [ AM → ; n p → ] làm vecto chỉ phương. Phương trình tham số của d:
GB
22 tháng 5
Dưới đây là hướng dẫn chi tiết giải bài toán từ link bạn cung cấp:
Đề bài
Trong không gian Oxyz, cho hai điểm \(A \left(\right. 3 ; 2 ; 1 \left.\right)\), \(M \left(\right. 3 ; 0 ; 0 \left.\right)\) và mặt phẳng \(\left(\right. P \left.\right) : x + y + z - 3 = 0\).
Viết phương trình của đường thẳng \(d\) đi qua điểm \(M\), nằm trong mặt phẳng \(\left(\right. P \left.\right)\) sao cho khoảng cách từ \(A\) đến đường thẳng \(d\) nhỏ nhất.
Phân tích & Cách giải
1. Điều kiện của đường thẳng \(d\)
- Đi qua \(M \left(\right. 3 ; 0 ; 0 \left.\right)\).
- Nằm trong mặt phẳng \(\left(\right. P \left.\right)\).
- Khoảng cách từ \(A\) đến \(d\) nhỏ nhất.
2. Nhận xét quan trọng
Khoảng cách từ \(A\) đến \(d\) nhỏ nhất khi đường thẳng \(d\) nằm trong \(\left(\right. P \left.\right)\), đi qua \(M\) và vuông góc với đoạn \(A M\).
3. Tìm vector chỉ phương của \(d\)
- \(\overset{\rightarrow}{A M} = \left(\right. 3 - 3 , 0 - 2 , 0 - 1 \left.\right) = \left(\right. 0 , - 2 , - 1 \left.\right)\)
- Đường thẳng \(d\) nằm trong \(\left(\right. P \left.\right)\) nên vector chỉ phương \(\overset{\rightarrow}{u}\) của \(d\) phải vuông góc với vector pháp tuyến của \(\left(\right. P \left.\right)\): \(\overset{\rightarrow}{n_{P}} = \left(\right. 1 , 1 , 1 \left.\right)\)
- Đồng thời, \(\overset{\rightarrow}{u}\) phải vuông góc với \(\overset{\rightarrow}{A M}\)
Vậy:
\(\overset{\rightarrow}{u} = \overset{\rightarrow}{A M} \times \overset{\rightarrow}{n_{P}}\)
Tính tích có hướng:
\(\overset{\rightarrow}{u} = \mid \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & - 2 & - 1 \\ 1 & 1 & 1 \mid = \mathbf{i} \left(\right. \left(\right. - 2 \left.\right) \cdot 1 - \left(\right. - 1 \left.\right) \cdot 1 \left.\right) - \mathbf{j} \left(\right. 0 \cdot 1 - \left(\right. - 1 \left.\right) \cdot 1 \left.\right) + \mathbf{k} \left(\right. 0 \cdot 1 - \left(\right. - 2 \left.\right) \cdot 1 \left.\right)\) \(= \mathbf{i} \left(\right. - 2 + 1 \left.\right) - \mathbf{j} \left(\right. 0 + 1 \left.\right) + \mathbf{k} \left(\right. 0 + 2 \left.\right) = \mathbf{i} \left(\right. - 1 \left.\right) - \mathbf{j} \left(\right. 1 \left.\right) + \mathbf{k} \left(\right. 2 \left.\right)\) \(\Rightarrow \overset{\rightarrow}{u} = \left(\right. - 1 , - 1 , 2 \left.\right)\)4. Viết phương trình tham số của \(d\)
Đường thẳng \(d\) đi qua \(M \left(\right. 3 ; 0 ; 0 \left.\right)\), nhận \(\overset{\rightarrow}{u} = \left(\right. - 1 , - 1 , 2 \left.\right)\) làm vector chỉ phương:
\(\boxed{\left{\right. x = 3 - t \\ y = 0 - t \\ z = 0 + 2 t \left(\right. t \in \mathbb{R} \left.\right)}\)Hoặc:
\(\boxed{\frac{x - 3}{- 1} = \frac{y}{- 1} = \frac{z}{2}}\)Kết luận
Phương trình đường thẳng \(d\) cần tìm là:
\(\boxed{\frac{x - 3}{- 1} = \frac{y}{- 1} = \frac{z}{2}}\)hoặc
\(\boxed{\left{\right. x = 3 - t \\ y = - t \\ z = 2 t}\)Nếu bạn cần giải thích thêm về các bước giải hoặc muốn biết cách tính khoảng cách, hãy hỏi nhé!