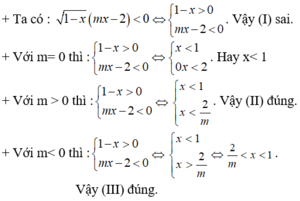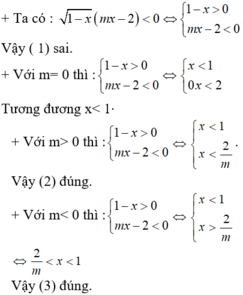Câu 1 : Tìm nghiệm nguyên âm nhỏ nhất thoả mãn bất phương trình (x - 1)√x(x+2) ≥ 0
Câu 2 : Bất phương trình \(\frac{1}{x+1}\) < \(\frac{1}{\left(x-1\right)^2}\) có tập nghiệm S là ??
Câu 3 : \(|\frac{2-x}{x+1}|\) ≥ 2 hỏi có bao nhiêu giá trị x thoả mãn bpt ??
∼ giải giúp mình với UwU∼