Số nguyên dương X (0<X <109) được gọi là số nguyên tố đặc biệt nếu X là số nguyên tố và các chữ số có trong X đều là số nguyên tố. ví dụ như 23 là số nguyên tố đặc biệt bởi vì 23 là số nguyên tố và 2, 3 củng là số nguyên tố. Nhập vào số nguyên dương X, Ghi ra giá trị X*2 nếu x là số nguyên tố đặc biệt, còn ngược lại ghi ra giá trị X div 2. Theo cach tập tin của pascal
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) ta có 1 = -1.(-1-0)
=> a là số nguyên dương vì = 1
=> b là số nguyên âm vì = -1
=> c là số không vì = 0

Tập hợp các số nguyên gồm:
A. Số nguyên âm, số 0 và số nguyên dương
B. Số 0 và các số nguyên âm
C. Số 0 vá các số nguyên dương
D. Số nguyên âm và các sô nguyên dương
A . số nguyên âm , số 0 và số nguyên dương


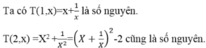
\Ta sẽ chứng minh T(1,x) là số nguyên
Thật vậy, áp dụng phép chứng minh quy nạp, Ta có:
Bước cơ sở: T(1,x) là số nguyên. Khẳng định đúng với n=1
Bước quy nạp: Giả sử T(n,x) là số nguyên với mọi n≥1. Ta sẽ chứng minh T(n+1,x) cũng là số nguyên
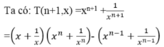
=T(1,x).T(n,x) – T(n-1,x).
Theo giả thuyết quy nạp, Ta có T(1,x),T(n,x), T(n-1,x) là các số nguyên nên T(n+1,x) là số nguyên
Chọn C



Để phương trình x^2 - 2m^2x - 4m - 1 = 0 có nghiệm nguyên, ta cần tìm giá trị của m sao cho delta (đại diện cho biểu thức bên trong căn bậc hai trong công thức nghiệm) là một số chính phương.
Công thức tính delta là: delta = b^2 - 4ac
Áp dụng vào phương trình đã cho, ta có:
a = 1, b = -2m^2, c = -4m - 1
delta = (-2m^2)^2 - 4(1)(-4m - 1)
= 4m^4 + 16m + 4
Để delta là một số chính phương, ta cần tìm các giá trị nguyên dương của m để đạt được điều kiện này. Ta có thể thử từng giá trị nguyên dương của m và kiểm tra xem delta có là số chính phương hay không.
Ví dụ, với m = 1, ta có:
delta = 4(1)^4 + 16(1) + 4
= 4 + 16 + 4
= 24
24 không phải là số chính phương.
Tiếp tục thử một số giá trị nguyên dương khác cho m, ta có:
Với m = 2, delta = 108 (không phải số chính phương)Với m = 3, delta = 400 (không phải số chính phương)Với m = 4, delta = 1004 (không phải số chính phương)Với m = 5, delta = 2016 (không phải số chính phương)Với m = 6, delta = 3484 (không phải số chính phương)Qua việc thử nghiệm, ta không tìm được giá trị nguyên dương của m để delta là một số chính phương. Do đó, không có giá trị của m thỏa mãn yêu cầu đề bài.
15:37
uses crt;
var x:int64;
kt,i,n,d,j,kt1,k:integer;
a:array[1..100]of longint;
st:string;
ktnt:boolean;
begin
clrscr;
write('x='); readln(x);
if (0<x) and (x<1000000000) then
begin
kt:=0;
for i:=2 to trunc(sqrt(x)) do
if x mod i=0 then kt:=1;
if kt=0 then
begin
str(x,st);
d:=length(st);
for j:=1 to d do
val(st[j],a[j],n);
ktnt:=false;
for j:=1 to d do
begin
kt1:=0;
for k:=2 to a[j]-1 do
if a[j] mod k=0 then kt1:=1;
if kt1=0 then ktnt:=true
else ktnt:=false;
end;
if ktnt=true then writeln(x*2)
else writeln(x div 2);
end
else writeln(x div 2);
end
else writeln('vui long nhap lai');
readln;
end.