Trên mặt phẳng cho n điểm phân biệt, trong đó có đúng 3 điểm thẳng hàng . Qua hai điểm ta vẽ một đoạn thẳng . Biết số đoạn thẳng là 171 đoạn thẳng. Tìm n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 10 2018
a)Lấy 1 điểm trong số 100 điểm đó.
Từ điểm đó kẻ với 99 điểm còn lại ta được 99 đoạn thẳng.
Vì có 100 điểm nên có100.99(đoạn thẳng).
Nhưng nếu tính như vậy thì số đoạn thẳng sẽ được lặp lại hai lần.
Vậy vẽ được tất cả số đoạn thẳng là:
100.99:2=4950(đoạn thẳng).
DP
8 tháng 7 2015
Vì trên mặt phẳng có 10 điểm mà không có 3 điểm nào thẳng hàng nên lấy một điểm bất kì nối với 9 điểm còn lại thì ta được 9 đường thẳng rồi điểm thứ hai thì có 8 đường thẳng .... cứ như thế cho đến điểm cuối cùng.
Nên số đường thẳng ta kẻ được từ 10 điểm trên một mặt phẳng mà khôn có 3 điểm nào thẳng hàng là:
10 x (10 - 1) : 2 = 45 ( đường thẳng)
Đáp số 45 đường thẳng
23 tháng 12 2016
a) Công thức tính số đường thẳng : \(\frac{n.\left(n-1\right)}{2}\) (n là số điểm)
Nếu không có 3 điểm thẳng hàng thì số đường thẳng kẻ được là :
\(\frac{2017.\left(2017-1\right)}{2}=2033136\)(đường thẳng)
Nếu là 7 điểm không thẳng hàng kẻ được số đường thẳng là :\(\frac{7.\left(7-1\right)}{2}=21\)(đường thẳng). Còn nếu là 7 điểm thẳng hàng thì chỉ kẻ được duy nhất 1 đường thẳng.
Số đường thẳng chênh lệch là :
21 - 1 = 20 (đường thẳng)
Số đường thẳng kẻ được từ 2017 điểm trong đó có 7 điểm thẳng hàng là :
2033136 - 20 = 2033116 (đường thẳng)
Đáp số : ..........................
b) Ta có : \(\frac{n.\left(n-1\right)}{2}=153\)
\(\Rightarrow n.\left(n-1\right)=153.2\)
\(n.\left(n-1\right)=306\)
\(n.\left(n-1\right)=2.3^2.17\)
\(n.\left(n-1\right)=18.17\)
\(\Rightarrow n=18\)
CM
29 tháng 11 2018
Đáp án là D
Gọi 10 điểm phân biệt đó là A1,A2,...,A10
Với A1 và 9 điểm còn lại ta kẻ được 9 đoạn thẳng
Với A2 và 9 điểm còn lại ta kẻ được 9 đoạn thẳng
…
Với A10 và 9 điểm còn lại ta kẻ được 9 đoạn thẳng
Vậy có tất cả 10.9 đoạn thẳng
Vì mỗi một đoạn thẳng được liệt kê 2 lần nên số đoạn thẳng phân biệt là: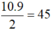 
đoạn thẳng
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 9 2023
Cứ hai điểm sẽ tạo thành một đoạn thẳng. Vậy với 10 điểm ta có:
10 cách chọn điểm thứ nhất, 9 cách chọn điểm thứ hai số đoạn thẳng được tạo là: 10 x 9 = 90
Theo cách tính trên mỗi đoạn thẳng được tính hai lần nên số đoạn thẳng là: 90 : 2 = 45 (đoạn thẳng)
Chon D.45