Ai giúp mik giải bài này theo cách LỚP 11 vs ạ mik cần CỰC KÌ GẤP Ạ:(((
Gọi K là tập hợp tất cả các giá trị của tham số m để phương trình sin2x + √2sin(x+π/4) - 2 = m CÓ ĐÚNG HAI NGHIỆM thuộc khoảng (0;3π/4). Tìm K ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
sin 2 x + 2 sin x + π 4 − 2 = m ( * ) ⇔ 2 sin x + π 4 2 2 sin x + π 4 = m + 3
Đặt t = 2 sin x + π 4 . Vì x ∈ 0 ; 3 π 4 nên t ∈ 0 ; 2 .
Khi đó phương trình (*) trở thành:
t 2 + t − m − 3 = 0 ( 1 )
Để phương trình (*) có đúng hai nghiệm thuộc khoảng 0 ; 3 π 4 phương trình (1) có đúng một nghiệm thuộc khoảng 0 ; 2
TH1
Δ = 0 0 < − b 2 a < 2 ⇔ 4 m + 4 = 0 0 < − 1 2 < 2 ( V L )
TH2
Δ > 0 f ( 0 ) f ( 2 ) < 0 ⇔ 4 m + 4 > 0 − m − 3 2 − 1 − m < 0 ⇔ m ∈ − 1 ; 2 − 1

Đáp án C.
Đặt t = sin x , t ∈ − 1 ; 1 . Phương trình đã cho trở thành 2 t + 1 t + 2 = m (*).
Để phương trình đã cho có đúng hai nghiệm thuộc đoạn 0 ; π thì phương trình (*) phải có đúng một nghiệm thuộc nửa khoảng 0 ; 1 .
Xét hàm số f t = 2 t + 1 t + 2 . Ta có f ' t = 3 t + 2 2 .
Bảng biến thiên của :
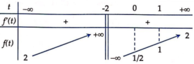
Vậy để phương trình (*) có đúng một nghiệm thuộc nửa khoảng 0 ; 1 thì m ∈ 1 2 ; 1 . Vậy C là đáp án đúng

Đặt t = sin x ∈ ( 0 ; 1 ] , ∀ x ∈ ( 0 ; π ) Phương trình trở thành: f(t)=m(1)
Ta cần tìm m để (1) có nghiệm thuộc khoảng ( 0 ; 1 ] ⇔ - 4 ≤ m < - 2
Chọn đáp án C.
\(sin2x+\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=m+2\)
\(\Leftrightarrow2sinx.cosx+sinx+cosx=m+2\)
Đặt \(sinx+cosx=t\) \(\left(0< t\le\sqrt{2}\right)\)
\(\Rightarrow2sinx.cosx=t^2-1\)
Pt trở thành:
\(t^2-1+t=m+2\Leftrightarrow t^2+t-3=m\) (1)
Dựa vào đường tròn lượng giác, để pt có đúng 2 nghiệm thuộc khoảng đã cho \(\Leftrightarrow\left(1\right)\) có 2 nghiệm thuộc \(\left(0;\frac{\sqrt{2}}{2}\right)\), hoặc \(\left(1\right)\) có nghiệm kép thuộc \(\left(\frac{\sqrt{2}}{2};1\right)\); hoặc (1) có 2 nghiệm thỏa mãn \(t_2< 0< \frac{\sqrt{2}}{2}\le t_1< 1\) hoặc (1) có 2 nghiệm phân biệt, trong đó \(\left\{{}\begin{matrix}t_1=1\\0< t_2< \frac{\sqrt{2}}{2}\end{matrix}\right.\)
Dựa vào đồ thị parabol, bạn tự biện luận nốt, nhiều trường hợp quá nhìn ngán vô cùng :D