Có tất cả bao nhiêu tập X {x∈N/-x3+4x =0 } thỏa mãn {1;2} ⊂ X ⊂{1;2;3;4;5} ?
A.8
B.1
C.3
D.6
Hứa sẽ tick giúp mình với.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
PT $\Leftrightarrow x^3+x+1-y(x^2-3)=0$
$\Leftrightarrow y=\frac{x^3+x+1}{x^2-3}$ (hiển nhiên $x^2-3\neq 0$ với mọi $x$ nguyên)
Để $y$ nguyên thì $\frac{x^3+x+1}{x^2-3}$ nguyên
$\Leftrightarrow x^3+x+1\vdots x^2-3$
$\Rightarrow x(x^2-3)+4x+1\vdots x^2-3$
$\Rightarrow 4x+1\vdots x^2-3$
Hiển nhiên $4x+1\neq 0$ nên $|4x+1|\geq x^2-3$
Nếu $x\geq \frac{-1}{4}$ thì $4x+1\geq x^2-3$
$\Leftrightarrow x^2-4x-4\leq 0$
$\Leftrightarrow (x-2)^2\leq 8<9$
$\Rightarrow -3< x-2< 3$
$\Rightarrow -1< x< 5$
$\Rightarrow x\in \left\{0; 1; 2; 3; 4\right\}$.
Nếu $x< \frac{-1}{4}$ thì $-4x-1\geq x^2-3$
$\Leftrightarrow x^2+4x-2\leq 0$
$\Leftrightarrow (x+2)^2-6\leq 0$
$\Leftrightarrow (x+2)^2\leq 6< 9$
$\Rightarrow -3< x+2< 3$
$\Rightarrow -5< x< 1$
$\Rightarrow x\in\left\{-4; -3; -2; -1\right\}$
Đến đây bạn thay vào tìm $y$ thôi

x 3 – 3 x 2 + 3 - x = 0 ⇔ x 2 . x – 3 . x 2 + ( 3 – x ) = 0 ⇔ x 2 ( x – 3 ) – ( x – 3 ) = 0 ⇔ ( x – 3 ) ( x 2 – 1 ) = 0
ó (x – 1)(x + 1)(x – 3) = 0
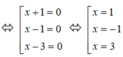
Vậy x = 1 hoặc x = 3 hoặc x = -1
Vậy có ba giá trị của x thỏa mãn đề bài
Đáp án cần chọn là:C

\(\left|x\right|+\left|y\right|=1=0+1\)
TH1: \(\left\{{}\begin{matrix}\left|x\right|=0\\\left|y\right|=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\pm1\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}\left|x\right|=1\\\left|y\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\pm1\\y=0\end{matrix}\right.\)

Ta có
x 3 + 2 x 2 – 9 x – 18 = 0 ⇔ ( x 3 + 2 x 2 ) – ( 9 x + 18 ) = 0 ⇔ x 2 ( x + 2 ) – 9 ( x + 2 ) = 0 ⇔ ( x + 2 ) ( x 2 – 9 ) = 0
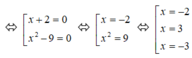
Vậy x = -2; x = 3; x =-3
Đáp án cần chọn là: D


(x + 6)(x - 9) = 0
\(\Rightarrow\) x + 6 = 0 hoặc x - 9 = 0
\(\Rightarrow\) x = - 6 hoặc x = 9
Tổng của chúng là - 6 + 9 = 3
B. vì -x^3+4x có 3 nghiệm là : 2,-2,0 mà chắc nghiệm 2 thỏa mãn điều kiện bài toán nên chỉ có 1 nghiệm đó là 2