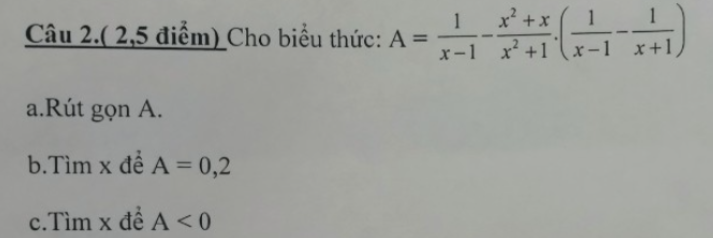xin chào mng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
6 tháng 5 2021
Trong LOGO để viết lên màn hình dòng chữ “Xin chào Việt Nam”, ta dùng câu lệnh:
A. LABEL { Xin chào Việt Nam}
C. PRINT {Xin chào Việt Nam}
B. LABEL [Xin chào Việt Nam]
D. PRINT [Xin chào Việt Nam]
HN
2
29 tháng 4 2022
a.\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\);\(ĐK:x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(A=\dfrac{1}{\left(x-1\right)}-\dfrac{2x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}\)
\(A=\dfrac{1}{x-1}-\dfrac{2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x-1}{x^2+1}\)
b.\(A=0,2=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow x^2+1=5x-5\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
c.\(A< 0\) mà \(x^2+1\ge1>0\)
--> A<0 khi \(x-1< 0\)
\(\Leftrightarrow x< 1\)
29 tháng 4 2022
a. -ĐKXĐ:\(x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{x^2+1}{\left(x^2+1\right)\left(x-1\right)}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\)
b. \(A=\dfrac{x-1}{x^2+1}=0,2\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{5\left(x-1\right)}{5\left(x^2+1\right)}=\dfrac{x^2+1}{5\left(x^2+1\right)}\)
\(\Rightarrow5x-5=x^2+1\)
\(\Leftrightarrow x^2-5x+1+5=0\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=3\left(nhận\right)\end{matrix}\right.\)
c. \(A=\dfrac{x-1}{x^2+1}< 0\)
\(\Leftrightarrow x-1< 0\) (vì \(x^2+1>0\forall x\))
\(\Leftrightarrow x< 1\)
NT
0
MA
2
23 tháng 12 2021
g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
23 tháng 12 2021
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
16 tháng 4 2023
IX
2. j
3. i
4. f
5. c
6. a
7. h
8. e
9. g
10. d
XI
2. part => parts
3. a => an
4. a => an
5. a => the
6. are => will be (không chắc lắm)
7. taking => take
8. are => is
C.
Bài 1
1. C
2. B
3. C
4. B
(Nên double-check trước khi chép)