Thả một hòn sỏi từ độ cao h xuống đất bỏ qua sức cản của không khí. Trong giây cuối cùng hòn sỏi rơi được 25m. Cho g = 10m/s2. Độ cao h bằng
A.90m B. 80m C. 40m D. 45m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
20 tháng 10 2018
Gọi độ cao ban đầu của viên sỏi là h (m) thời gian rơi hết độ cao h là t.
Ta có:
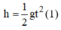
Quãng đường vật rơi được trước khi chạm đất 1 giây (tức là rơi được t’ = t -1 s) là:
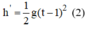
Theo đề ta có: h – h’ = 15 (3)
Thế (1), (2) vào (3)
16 tháng 4 2017
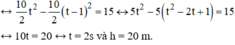
Trả lời:
Tương tự các bài trên.
- Gọi t là thời gian từ lúc rơi cho tới khi chạm đất.
Ta có: h = s = (quãng đường vật rơi) (1)
- Gọi h' là quãng đường vật rơi đến trước khi chạm đất 1 giây:
h' = s' = (t – 1)2. (2)
Gọi ∆h là quãng đường vật rơi (đi được) trong giây cuối cùng:
∆h = h - h' = 15m (3)
Thay (1), (2) vào (3):
=> -
(t2 – 2t + 1) = 15
=> gt - = 15 => t =
= 2s
Thay t = 2s vào (1) => h = = 20m.
6 tháng 10 2021
a) Chọn gốc thế năng tại mặt đất.
Cơ năng của vật tại vị trí ném: \(W_1=mgh_1+\dfrac{1}{2}mv_1^2\)
Cơ năng vật ở độ cao cực đại: \(W_2=mgh_2\)
Mà ta có: \(W_1=W_2\)
\(\Rightarrow mgh_1+\dfrac{1}{2}mv^2_1=mgh_2\) \(\Rightarrow gh_1+\dfrac{1}{2}v_1^2=gh_2\)
Với \(\left\{{}\begin{matrix}g=10\\h_1=40m\\v_1=10\end{matrix}\right.\) \(\Rightarrow h_2=45m\)
b) Ta vẫn chọn gốc thế năng tại vị trí cũ.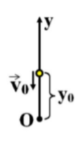 
\(y=y_0+v_0t-\dfrac{1}{2}gt^2=40-10t-\dfrac{1}{2}\cdot10\cdot t^2=0\)
( vì khi vật chạm đất thì y=0) \(\Rightarrow t=2s\)
c) Thời gian vật rơi khi chạm đất: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot40}{10}}=2\sqrt{2}s\)
Vận tốc vật khi chạm đất:
\(v=\sqrt{v^2_0+\left(gt\right)^2}=\sqrt{10^2+\left(10\cdot2\sqrt{2}\right)^2}=30\)m/s
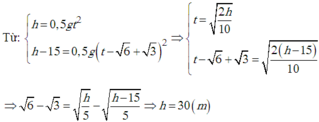
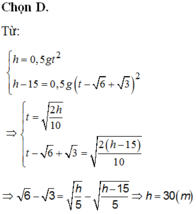
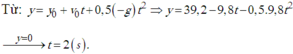
Thả một hòn sỏi từ độ cao h xuống đất bỏ qua sức cản của không khí. Trong giây cuối cùng hòn sỏi rơi được 25m. Cho g = 10m/s2. Độ cao h bằng
A.90m B. 80m C. 40m D. 45m
25=1\2.10.x2 -1\2.10(x-1)2
x=3 s
h=1\2.10.32
=>h=45 m
ok