Cho tam giác ABC cân tại A. Gọi tia AE là tia phân giác của góc ngoài tại đỉnh A. Chứng minh rằng AE // BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
0
23 tháng 6 2021
Kẻ \(AH\perp BC\) tại H
Áp dụng hệ thức lượng trong tam giác vuông BAC có:
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\)
Do AD và AE lần lượt là hai tia phân giác trong và ngoài tại đỉnh A
\(\Rightarrow AD\perp AE\)
Áp dụng hệ thức lượng vào tam giác vuông AED có:
\(\dfrac{1}{AE^2}+\dfrac{1}{AD^2}=\dfrac{1}{AH^2}\) (AH là đường cao của tam giác AED do \(AH\perp BC\) hay \(AH\perp ED\))
\(\Rightarrow\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AE^2}+\dfrac{1}{DA^2}\)
Vậy...
TH
12 tháng 1 2018
Chú ý:Góc ngoài tam giác bằng tổng số đo 2 góc trog tam giác không kể với nó
Vậy góc(A1)+góc(A2)=góc(B)+góc(C) .(1)
Do Am là tia phân giác ngoài tại đỉnh A của tam giác ABC nên góc A1=góc (A2).(2)
Lại có tam giác ABC cân tại A do(AB=AC) nên góc (B)=góc(C).(3)
Từ(1);(2) và (3) =>góc(A1)+góc (A1)=góc (C)+góc(C)
Suy ra góc( A1)=góc(C) mà 2 góc này nằm ở vị ttrí so le nhau
Do đó Am//BC . (dpcm)
10 tháng 1 2022
a: Ta có: ΔAMB cân tại A
mà AE là đường trung tuyến
nên AE là đường phân giác
b: Ta có: ΔAMB cân tại A
mà AE là đường trung tuyến
nên AE là đường cao
10 tháng 4 2022
a: Xét ΔBAK có
BE là đường cao
BE là đường trung tuyến
Do đó: ΔBAK cân tại B
b: Xét ΔBAD và ΔBKD có
BA=BK
\(\widehat{ABD}=\widehat{KBD}\)
BD chung
Do đó: ΔBAD=ΔBKD
Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)
HN
9 tháng 5 2022
a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :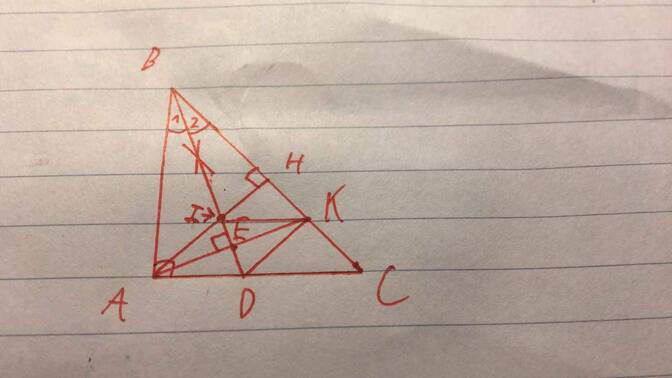
5 tháng 12 2023
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: ΔABD=ΔEBD
=>BA=BE và DA=DE
Xét ΔBAE có BA=BE
nên ΔBAE cân tại B
c: Ta có: DA=DE
DE<DC(ΔDEC vuông tại E nên DC là cạnh huyền)
=>DA<DC
d: BA=BE
=>B nằm trên đường trung trực của AE(1)
DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD vuông góc với AE tại trung điểm của AE
=>BD\(\perp\)AE tại M và M là trung điểm của AE
CG=2GM nên \(GM=\dfrac{1}{2}CG\)
CG+GM=CM
=>\(\dfrac{1}{2}CG+CG=CM\)
=>\(CM=\dfrac{3}{2}CG\)
=>\(CG=\dfrac{2}{3}CM\)
Xét ΔEAC có
CM là đường trung tuyến
\(CG=\dfrac{2}{3}CM\)
Do đó: G là trọng tâm của ΔEAC
Xét ΔEAC có
G là trọng tâm
N là trung điểm của EC
Do đó: A,G,N thẳng hàng
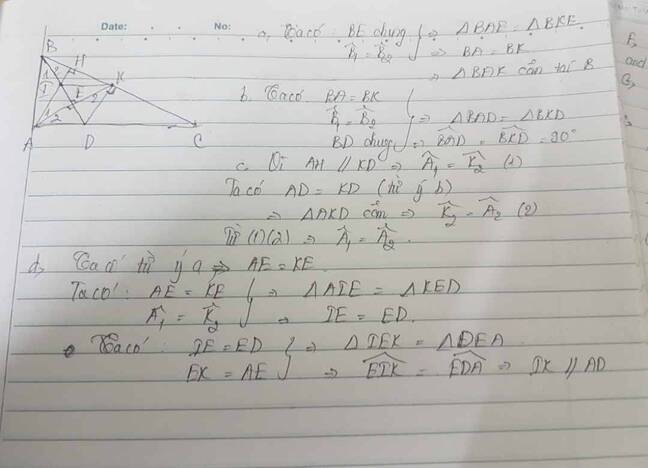
TH1: AE là tia pgiac góc B'AC (AB' là tia đối của tia AB)
Xét B'AC là góc ngoài tgiac ABC tại đỉnh A => góc B'AC = góc B + góc C
Mà tgiac ABC cân tại A => góc B = góc C
=> Góc C = 1/2 góc B'AC
Lại có AE là tia pgiac góc B'AC => góc EAC = 1/2 góc B'AC
=> Góc C = góc EAC
Mà hai góc này so le trong => AE song song BC.
cmtt với trường hợp AE là tia pgiac góc C'AB (AC' là tia đối của tia AC)
Vậy ta có đpcm.