Question

[Quỳnh Nguyễn Thị Ngọc]

1. Thầy chủ nhiệm có 16 cuốn sách đôi một khác nhau gồm 8 cuốn sách toán , 5 cuốn sách lý và 3 cuốn sách anh. Thầy lấy 8 cuốn tặng đều cho 8 bạn học sinh. Tính xác suất để sau khi tặng mỗi loại sách còn ít nhất một cuốn

2. Có 8 bạn cùng ngồi xung quanh một cái bàn tròn, mỗi bạn cầm một đồng xu như nhau. Tất cả 8 bạn cùng tung đồng xu của mình, bạn có đồng xu ngửa thì đứng, bạn có đồng xu sấp thì ngồi. Tính xác suất để không có hai bạn liền kề cùng đứng

Answer 1

[Nguyễn Việt Lâm]

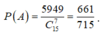
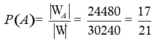
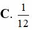
Câu 1:

Tổng trường hợp: \(N=A_{16}^8\)

- TH1: tặng hết 8 cuốn toán: \(8!\) cách

- TH2: tặng hết 5 cuốn Lý, 3 cuốn còn lại chọn ra từ 11 cuốn \(\Rightarrow C_{11}^3.8!\)

- TH3: tặng hết 3 cuốn Anh, 5 cuốn còn lại chọn ra từ 13 cuốn \(\Rightarrow C_{13}^5.8!\)

Phần bị trùng TH2 và TH3: tặng 5 cuốn Lý và 3 cuốn anh: \(8!\) cách

Tổng cộng: \(n=8!+C_{11}^3.8!+C_{13}^5.8!-8!=\left(C_{11}^3+C_{13}^5\right).8!\)

Xác suất: \(1-\frac{n}{N}=\)

Sao cái đống 8! kia cứ thừa thừa thế nào ấy nhỉ? :D

Câu 2:

Viết lại bài toán: có 8 bạn chưa rõ giới tính xếp vào bàn tròn, tính xác suất để ko có 2 bạn nữ nào ngồi cạnh nhau.

Để ko có 2 bạn nữ ngồi liền kề thì tối đa chỉ có 4 bạn nữ.

- TH1: đúng 1 bạn nữ, luôn đúng, có... cách xếp 1 bạn nữ vào bàn tròn và 7 bạn nam.

- TH2: 2 bạn nữ và 6 bạn nam, xếp 6 bạn nam tạo ra 6 khe trống, xếp 2 bạn nữ này vào 6 khe trống đó

- TH3: 3 bạn nữ, xếp 5 nam tạo 5 khe trống, xếp 3 nữ vào 5 khe trống

- TH4: nam nữ xen kẽ, có đúng 1 cách xếp