Tổng các sos nguyên x , thỏa mãn : (x2 + 5) . (x2 -25) = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 2 2022
bạn đăng tách ra cho mn giúp nhé
a, Để pt có 2 nghiệm pb
\(\Delta'=1-m\ge0\Leftrightarrow m\le1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-2\left(1\right)\\x_1x_2=m\left(2\right)\end{matrix}\right.\)
\(x_1-3x_2=0\)(3)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1-3x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_1=-2\\x_2=-2-x_1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{2}\\x_2=-\dfrac{3}{2}\end{matrix}\right.\)
Thay vào (2) ta được \(m=\left(-\dfrac{1}{2}\right)\left(-\dfrac{3}{2}\right)=\dfrac{3}{4}\)
16 tháng 2 2022
\(b,\Delta=\left(m+5\right)^2-4\left(-m+6\right)\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-7-4\sqrt{3}\\m\ge-7+4\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x1+x2=m+5\\2x1+3x2=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x1+2x2=2m+10\\2x1+3x2=13\end{matrix}\right.\)\(\)
\(\Rightarrow x2=13-2m-10=3-2m\Rightarrow x1=m+5-x2=m+5-3+2m=3m+2\)
\(x1x2=6-m\Rightarrow\left(3-2m\right)\left(3m+2\right)=6-m\Leftrightarrow\left[{}\begin{matrix}m=0\left(tm\right)\\m=1\left(tm\right)\end{matrix}\right.\)
\(c,\Delta'=\left(m+1\right)^2-\left(m^2-2m+29\right)\ge0\Leftrightarrow m\ge7\)
\(\Rightarrow\left\{{}\begin{matrix}x1+x2=2m+2\\x1=2x2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x2=\dfrac{2m+2}{3}\\x1=\dfrac{2\left(2m+2\right)}{3}\end{matrix}\right.\)
\(\Rightarrow x1.x2=\dfrac{\left(2m+2\right).2\left(2m+2\right)}{9}=m^2-2m+29\Leftrightarrow\left[{}\begin{matrix}m=11\left(tm\right)\\m=23\left(tm\right)\end{matrix}\right.\)
CM
25 tháng 2 2017
Ta có (1) ⇔ x 4 + x 2 + 20 = y 2 + y
Ta thấy: x 4 + x 2 < x 4 + x 2 + 20 ≤ x 4 + x 2 + 20 + 8 x 2 ⇔ x 2 ( x 2 + 1 ) < y ( y + 1 ) ≤ ( x 2 + 4 ) ( x 2 + 5 )
Vì x, y ∈ Z nên ta xét các trường hợp sau
+ TH1. y ( y + 1 ) = ( x 2 + 1 ) ( x 2 + 2 ) ⇔ x 4 + x 2 + 20 = x 4 + 3 x 2 + 2 ⇔ 2 x 2 = 18 ⇔ x 2 = 9 ⇔ x = ± 3
Với x 2 = 9 ⇒ y 2 + y = 9 2 + 9 + 20 ⇔ y 2 + y − 110 = 0 ⇔ y = 10 ; y = − 11 ( t . m )
+ TH2 y ( y + 1 ) = ( x 2 + 2 ) ( x 2 + 3 ) ⇔ x 4 + x 2 + 20 = x 4 + 5 x 2 + 6 ⇔ 4 x 2 = 14 ⇔ x 2 = 7 2 ( l o ạ i )
+ TH3: y ( y + 1 ) = ( x 2 + 3 ) ( x 2 + 4 ) ⇔ 6 x 2 = 8 ⇔ x 2 = 4 3 ( l o ạ i )
+ TH4: y ( y + 1 ) = ( x 2 + 4 ) ( x 2 + 5 ) ⇔ 8 x 2 = 0 ⇔ x 2 = 0 ⇔ x = 0
Với x 2 = 0 ta có y 2 + y = 20 ⇔ y 2 + y − 20 = 0 ⇔ y = − 5 ; y = 4
Vậy PT đã cho có nghiệm nguyên (x;y) là :
(3;10), (3;-11), (-3; 10), (-3;-11), (0; -5), (0;4).
PT
1
CM
20 tháng 12 2019
x(x – 1)(x + 1) + x 2 – 1 = 0
ó x(x – 1)(x + 1) + ( x 2 – 1) = 0
ó x(x – 1)(x + 1) + (x – 1)(x + 1) = 0
ó (x + 1)(x – 1)(x + 1) = 0
ó ( x + 1 ) 2 (x – 1) = 0
Vậy x = -1 hoặc x = 1
Tổng các giá trị của x là 1 + (-1) = 0
Đáp án cần chọn là: D
10 tháng 11 2021
\(1,\Leftrightarrow x^2-10x+25=0\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x=5\left(B\right)\\ 2,Giống.1\\ 3,=5x^2\left(B\right)\\ 4,x^3=x\Leftrightarrow x^3-x=0\\ \Leftrightarrow x\left(x^2-1\right)=0\\ \Leftrightarrow x\left(x-1\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\\ \Leftrightarrow A\)
TT
Trần Thị Khiêm
VIP
16 tháng 8
Đề bài:
Xét các số nguyên \(x_{1} , x_{2} , \ldots , x_{5}\) thỏa mãn
\(\left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots \left(\right. 1 + x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } \left(\right. 1 - x_{1} \left.\right) \left(\right. 1 - x_{2} \left.\right) \hdots \left(\right. 1 - x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } x .\)
Chứng minh rằng
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
Lời giải:
Gọi
\(P = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) , Q = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Theo đề: \(P = Q = x\).
Bước 1: Xét tích \(P Q\)
\(P Q = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) \left(\right. 1 - x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Bước 2: Sử dụng giả thiết \(P = Q\)
Từ \(P = Q\), suy ra:
\(\prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Chuyển vế:
\(& \prod_{i = 1}^{5} \frac{1 + x_{i}}{1 - x_{i}} = 1. & & (\text{1})\)
Bước 3: Phân tích trường hợp
- Nếu có một \(x_{i} = 1\), thì vế phải (1) có mẫu số bằng 0 → đẳng thức chỉ đúng khi đồng thời tử số cũng bằng 0, tức là có một \(x_{j} = - 1\).
Trong trường hợp này, trong tích \(P = \left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots\), sẽ có một thừa số bằng 0.
⇒ \(x = 0\).
Do đó \(x x_{1} x_{2} \hdots x_{5} = 0\). - Nếu có một \(x_{i} = - 1\), tương tự, \(x = 0\).
⇒ Kết quả đúng. - Nếu không có số nào bằng \(\pm 1\):
Khi đó (1) hoàn toàn xác định.
Lưu ý rằng \(\frac{1 + x_{i}}{1 - x_{i}}\) là một phân số không bằng 0.
Tích của 5 phân số bằng 1.
⇒ Có thể xảy ra, nhưng ta cần liên hệ với tích \(P Q\):
\(P Q = P^{2} = x^{2} = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Nếu không có số nào bằng \(\pm 1\), thì mỗi \(1 - x_{i}^{2} \neq 0\). Vế phải khác 0, suy ra \(x \neq 0\).
Nhưng khi đó \(x^{2} = \prod \left(\right. 1 - x_{i}^{2} \left.\right)\).
Nghĩa là \(x\) chia hết cho tích \(\prod x_{i}\) (do đồng dư mod \(x_{i}\), lập luận chia hết)…
Kết quả là hoặc \(x = 0\) hoặc một trong các \(x_{i} = 0\).
⇒ Trong cả hai trường hợp, \(x x_{1} x_{2} \hdots x_{5} = 0\).
Kết luận:
Dù xảy ra trường hợp nào thì ta luôn có:
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
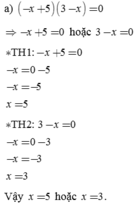
( x2 + 5 ) . ( x2 - 25 ) = 0
=> x2 + 5 = 0 or x2 - 25 = 0
+ TH1 : x2 + 5 = 0
x2 = 0 - 5
x2 = -5 ( vô lí )
+ TH2 : x2 - 25 = 0
x2 = 0 + 25
x2 = 25
x2 = 52
=> x = 5
Vậy x = 5
\(\orbr{\begin{cases}x^2+5=0\\x^2-25=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x^2=-5\left(vo.ly\right)\\x=5\end{cases}}\)
Vậy x=5