Chứng minh rằng:102+112+122=(12+1)2+(12+2)2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 1 12 + 1 13 + ... + 1 22 > 1 22 + 1 22 + ... + 1 22 ⏟ 11 s = 11 22 = 1 2

A = 1 12 + 1 13 + 1 14 + ... + 1 22 > 1 22 + 1 22 + ... 1 22 ⏟ 11 s = 11 22 = 1 2 .

A = 1 12 + 1 13 + 1 14 + ... + 1 22 > 1 2 ⇔ 1 12 + 1 13 + 1 14 + ... + 1 22 > 11 22 ⇔ 1 12 − 1 22 + 1 13 − 1 22 + 1 14 − 1 22 + ... + 1 22 − 1 22 > 0
Vì 1 12 > 0 , 1 13 > 0 , ... , 1 21 > 1 22 nên 1 12 − 1 22 > 0 , 1 13 − 1 22 > 0 , ... , 1 21 − 1 22 > 0 , 1 22 − 1 22 = 0
Suy ra A > 1 2

a) A = 1 12 + 1 13 + 1 14 + ... + 1 22 > 1 22 + 1 22 + ... 1 22 ⏟ 11 s = 11 22 = 1 2 .
b) B = 1 6 + ... 1 9 + 1 10 + ... + 1 19 < 1 4 + ... + 1 4 ⏟ 4 s o + 1 10 + ... + 1 10 ⏟ 10 s o = 2
c) C = 1 10 + 1 11 + ... + 1 100 > 1 10 + 1 100 = ... + 1 100 ⏟ 90 s o = 1 10 + 90 100 = 1

B=[2+(-7)]+[12+(-17)]+...+[102+(-107)]+112
B=-5+-5+...+-5+112
B=-5.503+112=-2403


Ta có:
\(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{150}>\dfrac{1}{150}+\dfrac{1}{150}+\dfrac{1}{150}+\dfrac{1}{150}+...+\dfrac{1}{150}\) (có 50 số hạng)
⇔ \(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{150}>\dfrac{1}{3}\) \(\left(1\right)\)
\(\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{200}>\dfrac{1}{200}+\dfrac{1}{200}+\dfrac{1}{200}+...+\dfrac{1}{200}\) (có 50 số hạng)
⇔ \(\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{200}>\dfrac{1}{4}\) \(\left(2\right)\)
Từ (1) và (2), cộng vế theo vế. Ta được:
\(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{150}+\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{200}>\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{7}{12}\)
⇒ \(ĐPCM\)
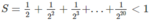
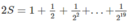
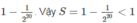
Mình thử nha :33
Ta có : \(10^2+11^2+12^2\)
\(=10^2+\left(12-1\right)^2+12^2\)
\(=10^2+12^2-2.12+1+12^2\)
\(=\left(12^2+2.12+1\right)+\left(12^2+4.12+4\right)+10^2-2.12-2.12-4.12-4\)
\(=\left(12+1\right)^2+\left(12+2\right)^2+100-8.12-4\)
\(=\left(12+1\right)^2+\left(12+2\right)^2\) (đpcm)
Cảm ơn bạn