tổng của 3 số dương x,y,z biết x/3 = y/4 =z/5 và 2x2 +2y2 -3z2 =- 100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DV
1
AH
Akai Haruma
Giáo viên
23 tháng 10 2023
Đoạn:
2x
2 + 2y
2 − 3z
2= -100 là như thế nào bạn nhỉ?
Bạn viết lại đề để mọi người hiểu hơn nhé.
7L
1
TC
4 tháng 4 2022
\(\dfrac{x}{4}=\dfrac{y}{4}=\dfrac{z}{5}=>\dfrac{2x^2}{32}=\dfrac{2y^2}{32}=\dfrac{3z^2}{75}\)
AD t/c của dãy tỉ số bằng nhâu ta có
\(\dfrac{2x^2}{32}=\dfrac{2y^2}{32}=\dfrac{3z^2}{75}=\dfrac{2x^2+2y^2-3z^2}{32+32-75}=\dfrac{-100}{-11}=\dfrac{100}{11}\)
\(=>\left[{}\begin{matrix}x=\dfrac{400}{11}\\y=\dfrac{400}{11}\\z=\dfrac{500}{11}\end{matrix}\right.\)
27 tháng 8 2021
Ta có: \(2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\)
Theo BĐT Bunhacopxky: \(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\Rightarrow\dfrac{3}{2}\left(x^2+y^2\right)\ge\dfrac{3}{4}\left(x+y\right)^2\\ \Rightarrow2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{5}{4}\left(x+y\right)^2\\ \Rightarrow\sqrt{2x^2+xy+2y^2}\ge\dfrac{\sqrt{5}}{2}\left(x+y\right)\)
Chứng minh tương tự:
\(\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}\left(y+z\right)\\ \sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}\left(x+z\right)\)
Cộng vế theo vế, ta được: \(P\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\cdot1=\sqrt{5}\)
Dấu "=" \(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
27 tháng 8 2021
Bạn tham khảo nhé
https://hoc24.vn/cau-hoi/cho-cac-so-duong-xyz-thoa-man-xyz1cmrcan2x2xy2y2can2y2yz2z2can2z2zx2x2can5.182722154737
LT
0
AH
Akai Haruma
Giáo viên
28 tháng 7
Lời giải:
Đặt $\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=k(k>0)$
$\Rightarrow x=3k; y=4k; z=5k$.
Khi đó:
$2x^2+2y^2-3z^2=-100$
$\Rightarrow 2(3k)^2+2(4k)^2-3(5k)^2=-100$
$\Rightarrow -25k^2=-100$
$\Rightarrow k^2=4\Rightarrow k=2$ (do $k>0$)
Ta có:
$x=3k=3.2=6; y=4k=4.2=8; z=5k=5.2=10$
NT
0
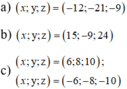
Lời giải:
Đặt $\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=k$
$\Rightarrow x=3k; y=4k ; z=5k$.
Khi đó:
$2x^2+2y^2-3z^2=-100$
$\Rightarrow 2(3k)^2+2(4k)^2-3(5k)^2=-100$
$\Rightarrow -25k^2=-100$
$\Rightarrow k^2=4\Rightarrow k=2$ (do $x,y,z$ dương nên $k$ phải dương)
$\Rightarrow x=3k=12; y=4k=16; z=5k=20$
Lời giải:
Đặt $\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=k$
$\Rightarrow x=3k; y=4k ; z=5k$.
Khi đó:
$2x^2+2y^2-3z^2=-100$
$\Rightarrow 2(3k)^2+2(4k)^2-3(5k)^2=-100$
$\Rightarrow -25k^2=-100$
$\Rightarrow k^2=4\Rightarrow k=2$ (do $x,y,z$ dương nên $k$ phải dương)
$\Rightarrow x=3k=12; y=4k=16; z=5k=20$