: Một ô tô chạy trên đường thẳng, lẩn lượt đi qua bốn điểm liên tiếp A, B, C, D cách đều nhau một khoảng 12km. Xe đi đoạn AB hết 20 min, đoạn BC hết 30 min, đoạn CD hết 20 min. Tính vận tốc trung bình trên mỗi đọan đường AB, BC, CD và trên cả quãng đường AD. Có thể biết chắc chắn sau 40 min kể từ khi ở A, xe ở vị trí nào không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức : vtb = \(\frac{\triangle x}{\triangle t}\) ta có :
+ Trên đoạn đường AB : vtb = \(\frac{12000}{20.600}=10\)m / s
+ Trên đoạn đường BC : vtb = \(\frac{12000}{30.60}\) = 6,67 m / s
+ Trên đoạn đường CD : vtb = \(\frac{12000}{20.60}\) = 10 m / s
+ Trên đoạn đường AD : vtb = \(\frac{12000.3}{\left(20+30+20\right).60}\) = 8,57 m /s
Không thể biết chắc chắn sau 40 min kể từ khi xe qua A , xe ở vị trí nào vì ta không biết được tính chất của chuyển động trên mỗi đoạn.

Đổi 20 phút = 1/3 giờ ; 30 phút = 1/2 giờ; 15 phút = 1/4 giờ ;
Vận tốc xe trên đoạn AB là :
12 : 1/3 = 36 (km/giờ)
Vận tốc xe trên đoạn đường BC là :
12 : 1/2 = 24 (km/giờ)
Vận tốc xe trên đoạn đường CD là :
12 : 1/4 = 48 (km/giờ)
Vận tốc của xe trên cả đoạn đường là :
(36 + 24 + 48) : 3 = 36 (km/giờ)
Áp dụng công thức Vtb=\(\frac{\Delta x}{\Delta t}\) ta có:
+ Trên đoạn đường AB: Vtb=\(\frac{12000}{20.60}=10m\) / s
+ Trên đoạn đường BC: Vtb=\(\frac{12000}{30.60}=6,67m\) / s
+ Trên đoạn đường CD: Vtb=\(\frac{12000}{20.60}=10m\) / s
+ Trên đoạn đường AD: Vtb=\(\frac{12000.3}{\left(20+30+20\right).60}=8,57m\) / s

Vận tốc TB đi trên đoạn AB:
v1=s1/t1=20/10=2(m/s)
Vận tốc TB đi trên quãng đường BC:
v2=s2/t2=350/20=17,5(m/s)
Vận tốc TB đi trên quãng đường AC là:
v(tb)=s(tổng):t(tổng)= (20+350):(10+20)\(\approx\) 12,333(m/s)
Vận tốc trung bình của xe đạp trên quãng đừng AB:
\(V=\dfrac{s}{t}\)=\(\dfrac{20}{10}=2\)(m/s)
Vận tốc trung bình của xe đạp trên quãng đường BC:
\(V=\dfrac{s}{t}=\dfrac{350}{20}=17,5\)(m/s)
Vận tốc trung bình của xe đạp trên cả quảng đường AC:
Vtb=\(\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{20+350}{10+20}=\dfrac{370}{30}=\dfrac{37}{3}\)

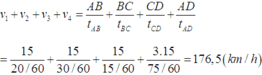
Lời giải: